
 函数
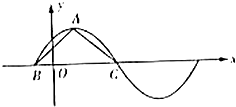
函数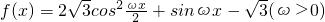 在一个周期内的图象如图,A为最高点,B,C为图象与x轴的交点,且
在一个周期内的图象如图,A为最高点,B,C为图象与x轴的交点,且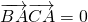 .
.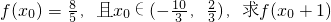 的值.
的值. ∵函数
∵函数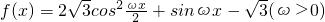 =
= (1+cosωx)+sinωx-
(1+cosωx)+sinωx- =2sin(ωx+
=2sin(ωx+ ),
),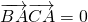 ,∴
,∴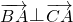 ,∴
,∴ BC=2,∴BC=4,故函数的周期为8,即
BC=2,∴BC=4,故函数的周期为8,即  =8,
=8, ,∴f(x)=2sin(
,∴f(x)=2sin( x+
x+ ),∴f(x)的值域为[-2,2].
),∴f(x)的值域为[-2,2].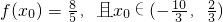 ,∴2sin(
,∴2sin( x0+
x0+ )=
)= ,sin(
,sin( x0+
x0+ )=
)= .
. x0+
x0+ )∈(-
)∈(- ,
, )可得 cos(
)可得 cos( x0+
x0+ )=
)= .
. (x0+1)+
(x0+1)+ ]=2sin[(
]=2sin[( x0+
x0+ )+
)+ ]=2sin (
]=2sin ( x0+
x0+ )cos
)cos +2cos (
+2cos ( x0+
x0+ )sin
)sin
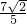 .
. ),根据两个向量垂直的条件求得,
),根据两个向量垂直的条件求得,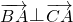 ,可得
,可得  BC=2,由此可得函数的周期为8,即
BC=2,由此可得函数的周期为8,即  =8.
=8. x+
x+ ),从而求得f(x)的值域.
),从而求得f(x)的值域. x0+
x0+ )=
)= ,cos(
,cos( x0+
x0+ )=
)= ,再根据 f(x0+1)=2sin[
,再根据 f(x0+1)=2sin[ (x0+1)+
(x0+1)+ ]=2sin[(
]=2sin[( x0+
x0+ )+
)+ ],利用两角和的正弦公式求得结果.
],利用两角和的正弦公式求得结果.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
| π |
| 6 |

查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 弹簧挂着的小球做上下运动,它在t秒时相对于平衡位置h厘米有下列关系确定h=2sin(t+
弹簧挂着的小球做上下运动,它在t秒时相对于平衡位置h厘米有下列关系确定h=2sin(t+| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com