
设定函数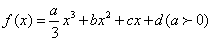 ,且方程
,且方程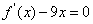 的两个根分别为1,4。
的两个根分别为1,4。
(Ⅰ)当a=3且曲线 过原点时,求
过原点时,求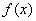 的解析式;
的解析式;
(Ⅱ)若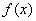 在
在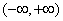 无极值点,求a的取值范围。
无极值点,求a的取值范围。
解:由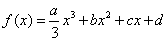 得
得 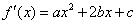
因为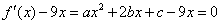 的两个根分别为1,4,
的两个根分别为1,4,
所以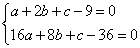 (*)
(*)
(Ⅰ)当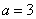 时,又由(*)式得
时,又由(*)式得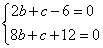
解得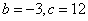
又因为曲线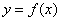 过原点,所以
过原点,所以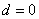
故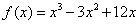
(Ⅱ)由于a>0,所以“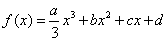 在(-∞,+∞)内无极值点”等价于“
在(-∞,+∞)内无极值点”等价于“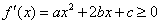 在(-∞,+∞)内恒成立”。
在(-∞,+∞)内恒成立”。
由(*)式得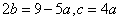 。
。
又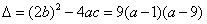
解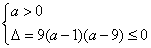 得
得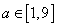
即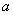 的取值范围
的取值范围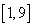
【命题意图】本题考查简单函数的求导计算求值问题和应用导数求解函数极值问题。在考查中又融入了对二次方程解法的考查。在对应用导数法求解函数极值问题的考查中主要以其逆向应用求参数为考查的重点,从而使问题增加了一定的难度。
【点评】高考中的函数问题每年都会考查有关导数的 应用问题,关于导数的应用在平时的学习中要能够熟练的掌握应用导数方法求解函数的单调性、极值、最值等问题的常规主法,且能够求解有关以上各个应用的逆向求参数问题。


科目:高中数学 来源:2012-2013学年江西省赣州市会昌中学高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
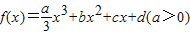 ,且方程f′(x)-9x=0的两个根分别为1,4.
,且方程f′(x)-9x=0的两个根分别为1,4.查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省吉安市白鹭洲中学高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
 ,且方程f′(x)-9x=0的两个根分别为1,4.
,且方程f′(x)-9x=0的两个根分别为1,4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com