Question

（08年湖南卷理）（本小题满分13分）

若A、B是抛物线上的不同两点，弦AB（不平行于y轴）的垂直平分线与

x轴相交于点P，则称弦AB是点P的一条“相关弦”.已知当时，点

存在无穷多条“相关弦”.给定.

（I）证明：点的所有“相关弦”的中点的横坐标相同；

(II) 试问：点的“相关弦”的弦长中是否存在最大值？

若存在，求其最大值（用x₀表示）：若不存在，请说明理由.

Answer 1

解: （I）设AB为点的任意一条“相关弦”，且点A、B的坐标分别是

,则,

两式相减得.因为x₁x₂,所以y₁+y₂0.

设直线AB的斜率是k，弦AB的中点是,则

k=.从而AB的垂直平分线l的方程为

又点P（x₀,0）在直线上，所以

而于是故点P（x₀,0）的所有“相关弦”的中点的横坐标都是x₀-2.

(Ⅱ)由(Ⅰ)知，弦AB所在直线的方程是，代入中，

整理得     （?）

则是方程（?）的两个实根，且

设点P的“相关弦”AB的弦长为l，则

   

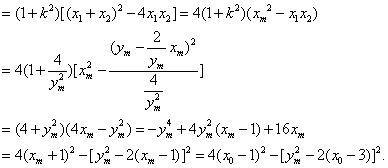
因为,于是设t=,则t(0,4x₀-8).

记^.

若,则,所以当,即=2(x₀-3)时,

l有最大值.

若,则,在区间上是减函数，

所以,l不存在最大值.

综上所述，当x₀>3时，点的“相关弦”的弦长中存在最大值，且最大值

为2（x₀-1）；当2< x₀3时，点的“相关弦”的弦长中不存在最大值.