
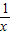 )-2lnx,g(x)=
)-2lnx,g(x)=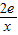 .(p是实数,e是自然对数的底数)
.(p是实数,e是自然对数的底数)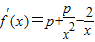 要使“f(x)为单调增函数”,转化为“f’(x)≥0恒成立”,再转化为“p≥
要使“f(x)为单调增函数”,转化为“f’(x)≥0恒成立”,再转化为“p≥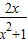 =
=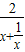 恒成立”,由最值法求解.同理,要使“f(x)为单调减函数”,转化为“f’(x)≤0恒成立”,再转化为“p≤
恒成立”,由最值法求解.同理,要使“f(x)为单调减函数”,转化为“f’(x)≤0恒成立”,再转化为“p≤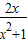 =
=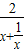 恒成立”,由最值法求解,最后两个结果取并集.
恒成立”,由最值法求解,最后两个结果取并集.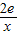 在[1,e]上为减函数,所以g(x)∈[2,2e],①当p≤0时,f(x)在[1,e]上递减;②当p≥1时,f(x)在[1,e]上递增;③当0<p<1时,两者作差比较.
在[1,e]上为减函数,所以g(x)∈[2,2e],①当p≤0时,f(x)在[1,e]上递减;②当p≥1时,f(x)在[1,e]上递增;③当0<p<1时,两者作差比较.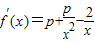 ,要使f(x)为单调增函数,须f’(x)≥0恒成立,
,要使f(x)为单调增函数,须f’(x)≥0恒成立,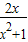 =
=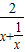 恒成立,又
恒成立,又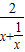 ≤1,
≤1,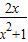 =
=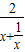 恒成立,又
恒成立,又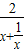 >0,所以当p≤0时,f(x)在(0,+∞)为单调减函数.
>0,所以当p≤0时,f(x)在(0,+∞)为单调减函数.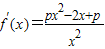 ,,∴f’(1)=2(p-1),设直线l:y=2(p-1)(x-1),
,,∴f’(1)=2(p-1),设直线l:y=2(p-1)(x-1),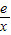 ,即(p-1)x2-(p-1)x-e=0
,即(p-1)x2-(p-1)x-e=0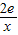 当p=1时,方程无解;当p≠1时由△=(p-1)2-4(p-1)(-e)=0,得p=1-4e,综上,p=1-4e
当p=1时,方程无解;当p≠1时由△=(p-1)2-4(p-1)(-e)=0,得p=1-4e,综上,p=1-4e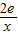 在[1,e]上为减函数,所以g(x)∈[2,2e]
在[1,e]上为减函数,所以g(x)∈[2,2e]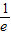 )-2lne>2⇒p>
)-2lne>2⇒p>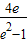 ③当0<p<1时,因x-
③当0<p<1时,因x-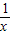 ≥0,x∈[1,e]
≥0,x∈[1,e]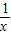 )-2lnx≤(x-
)-2lnx≤(x-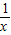 )-2lnx≤e-
)-2lnx≤e-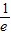 -2lne<2不合题意
-2lne<2不合题意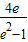 ,+∞)
,+∞)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
| p |
| q |
| p |
| q |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 2e |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 2e |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 )-2lnx,g(x)=
)-2lnx,g(x)=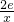 (p是实数,e为自然对数的底数)
(p是实数,e为自然对数的底数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com