
已知数列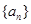 中,
中, 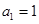 ,且
,且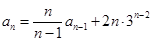
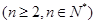 .
.
(1) 求数列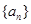 的通项公式;
的通项公式;
(2) 令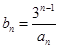
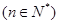 ,数列
,数列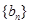 的前
的前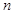 项和为
项和为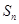 ,试比较
,试比较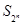 与
与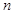 的大小;
的大小;
(3) 令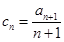
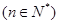 ,数列
,数列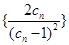 的前
的前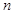 项和为
项和为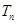 .求证:对任意
.求证:对任意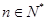 ,
,
都有 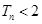 .
.
(1) 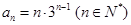 . (2)当
. (2)当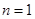 时,
时,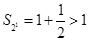 ;当
;当 时,
时,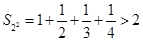 ;当
;当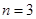 时,
时,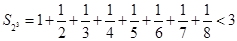 .
.
猜想当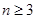 时,
时,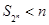 . (3)略
. (3)略
【解析】已知数列的项与和的递推关系求数列的通项时,一般通过仿写构造一个新等式,两个式子相减得到项的递推关系,再据递推关系的特点选择合适的求通项方法;求数列的前n项和,关键是根据数列通项的特点选择合适的求和方法
(1)将已知的和与项的递推关系中的n用n-1代替,仿写出一个新的等式,两个式子相减,利用等差数列的定义得到一个等差数列,利用等差数列的通项公式求出通项.
(2)由于数列的通项是一个等差数列与一个等比数列的乘积构成的新数列,利用错位相减法求出数列的前n项和
(3)因为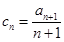 ,对于n分类讨论的得到前n项和
,对于n分类讨论的得到前n项和


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源:2015届云南省高一下学期期中考试数学试卷(解析版) 题型:选择题
已知数列 中, a2=7,且an =an+1-6(n∈
中, a2=7,且an =an+1-6(n∈ ),则前n项和Sn=" (" )
),则前n项和Sn=" (" )
A. B. n2 C.
B. n2 C. D.3n2
–2n
D.3n2
–2n
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com