
| 1 | 2 |
| ||||||
|
| 9 |
| 15 |
| 3 |
| 5 |
(
| ||||||
|
| 2n(n!)2 |
| (2n!) |
| 2n-1[(n-1)!]2 |
| [2(n-1)]! |
| 2n-1[(n-1)!]2 |
| 2[(n-1)]! |
| n-1 |
| 2n-1 |
| n-1 |
| 2n-1 |
| n-1 |
| 2(n-1)+1 |
| 1 |
| 2 |
| 2n-1[(n-1)!]2 |
| 2[(n-1)]! |
2n-2
| ||
|
| 1 |
| 2 |


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:2009-2010学年浙江省嘉兴一中高二(上)期中数学试卷(理科)(解析版) 题型:解答题
 (其中n≥3 ).
(其中n≥3 ).查看答案和解析>>
科目:高中数学 来源:浙江省嘉兴市第一中学09-10学年高二第一学期期中考试理) 题型:解答题
现假设红色球与黑色各有n个,且互不相同。
(1)当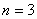 时,若将这些球放入3个不同的盒子中,每个盒子至少有一个球,则有多少种不同的放法?
时,若将这些球放入3个不同的盒子中,每个盒子至少有一个球,则有多少种不同的放法?
(2)当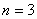 时,若将这些球随机的配成3对,则至少有一对球的颜色一样的概率是多少?
时,若将这些球随机的配成3对,则至少有一对球的颜色一样的概率是多少?
(3)将这些球随机的配成n对,记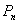 为至少有一对球的颜色一样的概率,
为至少有一对球的颜色一样的概率,
求证: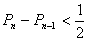 (其中
(其中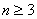 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com