
设集合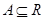 ,如果
,如果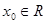 满足:对任意
满足:对任意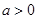 ,都存在
,都存在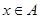 ,使得
,使得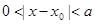 ,那么称
,那么称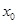 为集合
为集合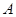 的一个聚点,则在下列集合中:(1)
的一个聚点,则在下列集合中:(1)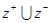 ;(2)
;(2)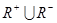 ;(3)
;(3)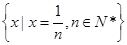 ;(4)
;(4)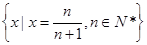 ,以
,以 为聚点的集合有
为聚点的集合有
(写出所有你认为正确的结论的序号).
(2)(3)
【解析】
试题分析:根据集合聚点的新定义,我们逐一分析四个集合中元素的性质,并判断是否满足集合聚点的定义,进而得到答案. :(1)对于某个a<1,比如a=0.5,此时对任意的x∈Z+∪Z-,都有|x-0|=0或者|x-0|≥1,也就是说不可能0<|x-0|<0.5,从而0不是Z+∪Z-的聚点;(2)集合{x|x∈R,x≠0},对任意的a,都存在x=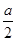 ,(实际上任意比a小得数都可以),使得0<|x|=
,(实际上任意比a小得数都可以),使得0<|x|=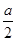 <a,∴0是集合{x|x∈R,x≠0}的聚点;(4)中,集合
<a,∴0是集合{x|x∈R,x≠0}的聚点;(4)中,集合 中的元素是极限为1的数列,除了第一项0之外,其余的都至少比0大
中的元素是极限为1的数列,除了第一项0之外,其余的都至少比0大
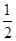 ∴在a<
∴在a<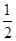 的时候,不存在满足得0<|x|<a的x,∴0不是集合
的时候,不存在满足得0<|x|<a的x,∴0不是集合 的聚点;(3)集合
的聚点;(3)集合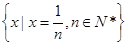 中的元素是极限为0的数列,对于任意的a>0,存在n>
中的元素是极限为0的数列,对于任意的a>0,存在n>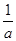 ,使0<|x|=
,使0<|x|=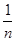 <a,∴0是集合
<a,∴0是集合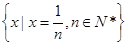 的聚点故答案为(2)(3)
的聚点故答案为(2)(3)
考点:集合元素的性质
点评:本题的考点是函数恒成立问题,主要考查的知识点是集合元素的性质,其中正确理解新定义--集合的聚点的含义,是解答本题的关键


科目:高中数学 来源:2013-2014学年江西省高三年级第四次同步考试理科数学试卷(解析版) 题型:填空题
设集合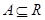 ,如果
,如果 满足:对任意
满足:对任意 ,都存在
,都存在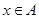 ,使得
,使得 ,那么称
,那么称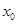 为集合
为集合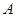 的一个聚点,则在下列集合中:(1)
的一个聚点,则在下列集合中:(1)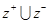 ;(2)
;(2)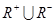 ;(3)
;(3)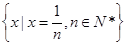 ;(4)
;(4) ,以
,以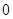 为聚点的集合有 (写出所有你认为正确的结论的序号).
为聚点的集合有 (写出所有你认为正确的结论的序号).
查看答案和解析>>
科目:高中数学 来源:2014届甘肃天水一中高二下学期期末考试理科数学试卷(解析版) 题型:填空题
设集合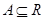 ,如果
,如果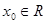 满足:对任意
满足:对任意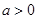 ,都存在
,都存在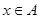 ,使得
,使得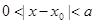 ,那么称
,那么称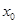 为集合
为集合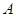 的一个聚点,则在下列集合中:(1)
的一个聚点,则在下列集合中:(1)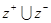 ;(2)
;(2)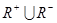 ;(3)
;(3)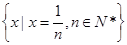 ;(4)
;(4)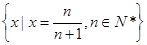 ,以
,以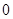 为聚点的集合有
为聚点的集合有
(写出所有你认为正确的结论的序号).
查看答案和解析>>
科目:高中数学 来源:2014届甘肃天水一中高二下学期期末考试文科数学试卷(解析版) 题型:填空题
设集合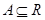 ,如果
,如果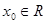 满足:对任意
满足:对任意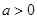 ,都存在
,都存在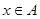 ,使得
,使得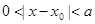 ,那么称
,那么称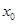 为集合
为集合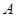 的一个聚点,则在下列集合中:(1)
的一个聚点,则在下列集合中:(1)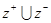 ;(2)
;(2) ;(3)
;(3)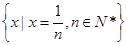 ;(4)
;(4)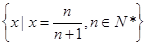 ,以
,以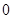 为聚点的集合有
为聚点的集合有
(写出所有你认为正确的结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
设集合![]() ,如果
,如果![]() 满足:对任意
满足:对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() ,那么称
,那么称![]() 为集合
为集合![]() 的一个聚点,则在下列集合中:(1)
的一个聚点,则在下列集合中:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() ,以
,以![]() 为聚点的集合有 .
为聚点的集合有 .
(写出所有你认为正确的结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com