
设数列{an}、{bn}、{cn}满足:bn=an-an+2,cn=an+2an+1+3an+2(n=1,2,3,…),求证:{an}为等差数列的充分必要条件是{cn}为等差数列且bn≤bn+1(n=1,2,3,…).
见解析
【解析】必要性:
设{an}是公差为d1的等差数列,则
bn+1-bn=(an+1-an+3)-(an-an+2)
=(an+1-an)-(an+3-an+2)=d1-d1=0,
所以bn≤bn+1(n=1,2,3,…)成立.
又cn+1-cn=(an+1-an)+2(an+2-an+1)+3(an+3-an+2)=d1+2d1+3d1=6d1(常数)(n=1,2,3,…),
所以数列{cn}为等差数列.
充分性:
设数列{cn}是公差为d2的等差数列,且bn≤bn+1(n=1,2,3,…).
∵cn=an+2an+1+3an+2,①
∴cn+2=an+2+2an+3+3an+4,②
①-②,得cn-cn+2=(an-an+2)+2(an+1-an+3)+3(an+2-an+4)=bn+2bn+1+3bn+2.
∵cn-cn+2=(cn-cn+1)+(cn+1-cn+2)=-2d2,
∴bn+2bn+1+3bn+2=-2d2,③
从而有bn+1+2bn+2+3bn+3=-2d2,④
④-③,得(bn+1-bn)+2(bn+2-bn+1)+3(bn+3-bn+2)=0.⑤
∵bn+1-bn≥0,bn+2-bn+1≥0,bn+3-bn+2≥0,
∴由⑤得bn+1-bn=0(n=1,2,3,…).
由此不妨设bn=d3(n=1,2,3,…),则an-an+2=d3(常数).
由此cn=an+2an+1+3an+2?cn=4an+2an+1-3d3,
从而cn+1=4an+1+2an+2-5d3,
两式相减得cn+1-cn=2(an+1-an)-2d3,
因此an+1-an=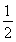 (cn+1-cn)+d3=
(cn+1-cn)+d3=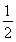 d2+d3(常数)(n=1,2,3,…),
d2+d3(常数)(n=1,2,3,…),
∴数列{an}为等差数列.


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第七章第3课时练习卷(解析版) 题型:填空题
用数学归纳法证明“当n为正偶数时xn-yn能被x+y整除”第一步应验证n=________时,命题成立;第二步归纳假设成立应写成____.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第七章第2课时练习卷(解析版) 题型:填空题
已知向量m=(1,1)与向量n=(x,2-2x)垂直,则x=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第七章第1课时练习卷(解析版) 题型:解答题
已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P为椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线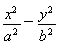 =1写出具有类似特性的性质,并加以证明.
=1写出具有类似特性的性质,并加以证明.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第一章第3课时练习卷(解析版) 题型:解答题
已知命题p:函数y=loga(1-2x)在定义域上单调递增;命题q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立.若p∨q是真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第一章第2课时练习卷(解析版) 题型:填空题
设全集I=R,已知集合M=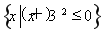 ,N={x|x2+x-6=0}.
,N={x|x2+x-6=0}.
(1)求(∁IM)∩N;
(2)记集合A=(∁IM)∩N,已知集合B={x|a-1≤x≤5-a,a∈R},若B∪A=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第一章第1课时练习卷(解析版) 题型:解答题
已知A={a+2,(a+1)2,a2+3a+3}且1∈A,求实数a的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1达标检测第2讲练习卷(解析版) 题型:填空题
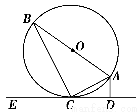
如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com