
如图,
ABCD是空间四边形,设△ABD和△CBD的重心分别为P、Q.求证:PQ∥平面ABC,PQ∥平面ADC.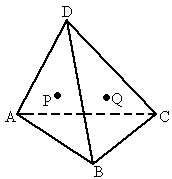
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源:训练必修二数学人教A版 人教A版 题型:044
如图,ABCD是一个正方形,E、F分别是AB和BC的中点,沿折痕DE、EF、FD折起得到一个空间几何体,请你动手折一折,看看这个空间几何体是什么几何体.

查看答案和解析>>
科目:高中数学 来源:训练必修二数学苏教版 苏教版 题型:044
如图,ABCD是一个正方形,E、F分别是AB和BC的中点,沿折痕DE、EF、FD折起得到一个空间几何体,请你动手折一折,看看这个空间几何体是什么几何体?
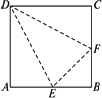
查看答案和解析>>
科目:高中数学 来源: 题型:
如![]() 图,ABCD是空间四边形,E、F、G、H分别是四边上的点,它们共面,并且AC∥平面EFGH,
图,ABCD是空间四边形,E、F、G、H分别是四边上的点,它们共面,并且AC∥平面EFGH,![]() BD∥平面EFGH,AC=m,BD=n,当EFGH是菱形时,AE∶EB=______.
BD∥平面EFGH,AC=m,BD=n,当EFGH是菱形时,AE∶EB=______.
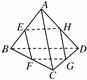
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com