练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知直线l:kx-y+2-k=0，双曲线C：x2-2y2=4，当k为何值时：

    （1）l与C无共点；

    （2）l与C有唯一公共点；

    （3）l与C有两个不同的公共点.

    思路解析：直线与双曲线公共点的个数就是直线与双曲线方程所组成的方程组解的个数，从而问题可转化为由方程组的解的个数来确定参数k的取值.

    解：（1）将直线与双曲线方程联立

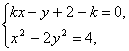    消去y,得

    （1-4k2）x2-8k(2-k)x-4(k2-4k+5)=0.    ①

    要使l与C无公共点，即方程无实数解，于是有Δ＜0，

    即64k2(2-k)2+16(1-4k2)(k2-4k+5)＜0.

    解得k＞或k＜.

    故当k＞或k＜时，l与C无公共点.

    （2）当1-4k2=0,即k=±时，显然方程①只有一解；

    又当Δ=0时，即k=时，方程①只有一解.

    故当k=±或k=时，l与C有唯一公共点.

    （3）当（1-4k2）≠0且Δ＞0时，方程有两解，即l与C有两个公共点，于是可得

    ＜k＜且k≠±.

    深化升华

        直线l:y=kx+m(m≠0),双曲线C：-=1,消去y得（b2-a2k2）x2-2a2mkx-a2m2-a2b2=0.则当b2-a2k2=0时，即k=±，l与C只有一个公共点；当b2-a2k2≠0时，Δ＞0l与C有两个公共点；Δ=0l与C只有一个公共点；Δ＜0l与C没有公共点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知直线l：y=kx+1与抛物线C：y2=x，则“k≠0”是“直线l与抛物线C有两个不同交点”的
    必要而不充分条件
    必要而不充分条件
    条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，已知圆M：（x+1）2+y2=8及定点N（1，0），点P是圆M上一动点，点Q为PN的中点，PM上一点G满足
    GQ
    •
    NP
    =0
    （1）求点G的轨迹C的方程；
    （2）已知直线l：y=kx+m与曲线C交于A、B两点，E（0，1），是否存在直线l，使得点N恰为△ABE的垂心？若存在，求出直线l的方程，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•海淀区一模）已知圆M：（x-
    		2
    ）2+y2=
    7
    3
    ，若椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的右顶点为圆M的圆心，离心率为
    		2
    2
    ．
    （I）求椭圆C的方程；
    （II）已知直线l：y=kx，若直线l与椭圆C分别交于A，B两点，与圆M分别交于G，H两点（其中点G在线段AB上），且|AG|=|BH|，求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线l:kx-y+1+2k=0.

    (1)证明直线l过定点;

    (2)若直线l交x轴负半轴于A，交y轴正半轴于B,△AOB的面积为S，试求S的最小值并求出此时直线l的方程.

    查看答案和解析>>

    同步练习册答案