
在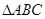 中,已知
中,已知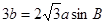 ,
,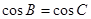 ,则
,则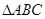 的形状是( )
的形状是( )
A. 直角三角形 B. 等腰三角形 C. 等边三角形 D. 等腰直角三角形
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都市高新区高三2月月考理科数学试卷(解析版 题型:填空题
已知椭圆方程为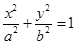 (
(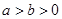 ),F
),F (-c,0)和F
(-c,0)和F (c,0)分别是椭圆的左 右焦点.
(c,0)分别是椭圆的左 右焦点.
①若P是椭圆上的动点,延长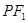 到M,使
到M,使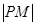 =
=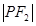 ,则M的轨迹是圆;
,则M的轨迹是圆;
②若P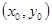 是椭圆上的动点,则
是椭圆上的动点,则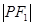
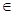
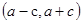 ;
;
③以焦点半径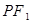 为直径的圆必与以长轴为直径的圆内切;
为直径的圆必与以长轴为直径的圆内切;
④若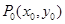 在椭圆
在椭圆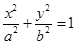 上,则过
上,则过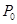 的椭圆的切线方程是
的椭圆的切线方程是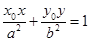 ;
;
⑤点P为椭圆上任意一点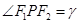 ,则椭圆的焦点角形的面积为
,则椭圆的焦点角形的面积为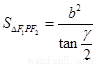 .
.
以上说法中,正确的有
查看答案和解析>>
科目:高中数学 来源:2014届山西省高二第一次月考理科数学试卷(解析版) 题型:选择题
已知结论:在正三角形ABC中,若D是边BC的中点,G是三角
形ABC的重心,则AG:GD=2:1,若把该结论推广到空间中,则有结论:在棱长都相等的
四面体ABCD中,若三角形BCD的中心为M,四面体内部一点O到各面的距离都相等,
则AO:OM=( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com