
分析 (1)由导数性质求出f(x)=-x2+7x,由点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,求出${S}_{n}=-{n}^{2}+7n$,由此能求出数列{an}的通项公式.
(2)令an=-2n+8≥0,得n≤4,由此能求出Sn的最大值.
解答 解:(1)∵f(x)=ax2+bx(a≠0),∴f′(x)=2ax+b,
∵函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,
∴a=-1,b=7,
∴f(x)=-x2+7x,
又∵点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
∴${S}_{n}=-{n}^{2}+7n$,
当n=1时,a1=S1=6,
当n≥2时,an=Sn-Sn-1=-2n+8,
∴an=-2n+8,n∈N*.
(2)令an=-2n+8≥0,得n≤4,
∴当n=3或n=4时,Sn取得最大值${S}_{3}={S}_{4}=-{3}^{2}+7×3$=12.
点评 本题考查数列的通项公式和数列前n项和的最大值的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
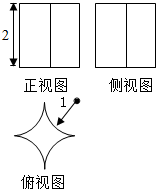 已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为8+2π.
已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为8+2π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  圆形区域 | |
| B. |  等腰三角形两腰与半椭圆围成的区域 | |
| C. | 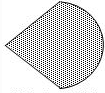 等腰三角形两腰与半圆围成的区域 | |
| D. | 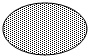 椭圆形区域 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 单调递增函数 | B. | 单调递减函数 | C. | 先减后增函数 | D. | 先增后减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
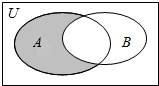 设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则图中阴影部分表示的集合为( )
设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则图中阴影部分表示的集合为( )| A. | {1,2,5,6} | B. | {1} | C. | {2} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
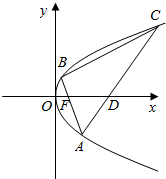 已知抛物线T:y2=2px(p>0)的焦点为F,A(x0,y0)为T上异于原点的任意一点,点D为x的正半轴上的点,且有|FA|=|FD|,若x0=3时,D的横坐标为5.
已知抛物线T:y2=2px(p>0)的焦点为F,A(x0,y0)为T上异于原点的任意一点,点D为x的正半轴上的点,且有|FA|=|FD|,若x0=3时,D的横坐标为5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com