
 解:①设此山高h(m),则
解:①设此山高h(m),则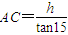 ,
,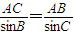 ,
,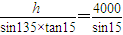 ,
,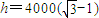 (m).
(m).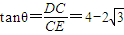 .
.

科目:高中数学 来源: 题型:
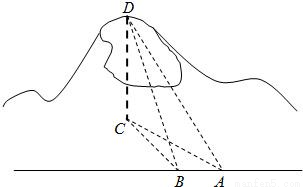
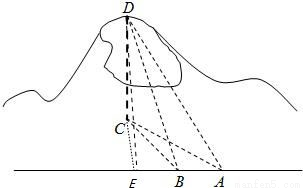
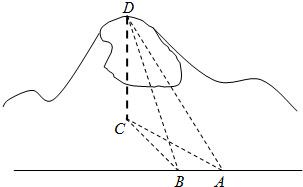 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北30°的方向上,仰角为15°,行驶4km后到达B处,测得此山顶在西偏北45o的方向上.
如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北30°的方向上,仰角为15°,行驶4km后到达B处,测得此山顶在西偏北45o的方向上.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,一辆汽车从O点出发,沿海岸一条直线公路以100千米/时的速度向东匀速行驶,汽车开动时,在O点南偏东方向距O点500千米且与海岸距离MQ为300千米的海上M处有一快艇,与汽车同时出发,要把一件重要的物品递送给这辆汽车的司机,问快艇至少须以多大的速度行驶,才能把物品递送到司机手中,并求快艇以最小速度行驶时的方向与OM所成的角.
如图,一辆汽车从O点出发,沿海岸一条直线公路以100千米/时的速度向东匀速行驶,汽车开动时,在O点南偏东方向距O点500千米且与海岸距离MQ为300千米的海上M处有一快艇,与汽车同时出发,要把一件重要的物品递送给这辆汽车的司机,问快艇至少须以多大的速度行驶,才能把物品递送到司机手中,并求快艇以最小速度行驶时的方向与OM所成的角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
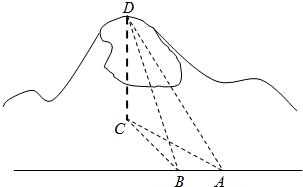 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北30°的方向上,仰角为15°,行驶4km后到达B处,测得此山顶在西偏北45o的方向上.
如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北30°的方向上,仰角为15°,行驶4km后到达B处,测得此山顶在西偏北45o的方向上.查看答案和解析>>
科目:高中数学 来源:2011年高考数学综合复习试卷(2)(解析版) 题型:解答题
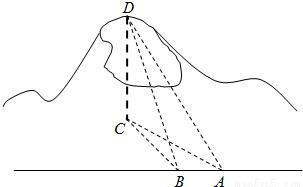
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com