【答案】
分析:(1)本题是一个指数型函数式的大小比较,这种题目需要先把底数化成相同的形式,化底数为2,根据函数是一个递增函数,写出指数之间的关系,得到未知数的范围.
(2)由已知得
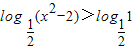
,由对数函数的单调性,我们可将原不等式化为一个二次不等式,解不等式求出x的取值范围,即可得到答案.
解答:解:(1)
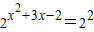
⇒x
2+3x-2=2⇒x
2+3x-4=0⇒x=1或x=-4
∴原方程的解集为{1,-4}
(2)解:
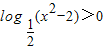
⇒
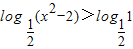
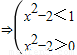
∴
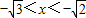
或
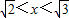
故原不等式的解集为
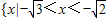
或
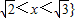 点评:
点评:本题考查指数、对数函数的单调性,解题的关键是把题目变化成能够利用函数的性质的形式,即把底数化成相同的形式.

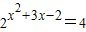
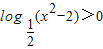 .
.