练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知四棱锥的三视图如图K40­11所示，则该四棱锥的五个面的最大面积是(　　)

    A．3  B．6  C．8  D．10


    C　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    平面直角坐标系xOy中，直线x－y＋1＝0截以原点O为圆心的圆所得的弦长为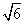

    (1)求圆O的方程．

    (2)若直线l与圆O切于第一象限，且与坐标轴交于D，E，当DE长度最小时，求直线l的方程．

    (3)设M，P是圆O上任意两点，点M关于x轴对称的点为N，若直线MP，NP分别交x轴于点(m，0)和(n，0)，问mn是否为定值？若是，请求出该定值；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    证明不等式1＋＋＋…＋<2 (n∈N*)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直三棱柱ABC ­ A1B1C1的底面为等腰直角三角形，∠BAC＝90°，AB＝AC＝2，AA1＝2 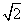，E，F分别是BC，AA1的中点．求：

    (1)异面直线EF和A1B所成的角；

    (2)三棱锥A ­ EFC的体积．

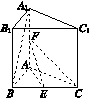
    图K41­6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个四棱锥的底面为菱形，其三视图如图K40­6所示，则这个四棱锥的体积是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     一个几何体的三视图如图K40­15所示，则该几何体的表面积是(　　)

    A．18＋2 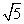  B．24＋2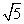

    C．24＋4 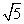  D．36＋4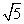

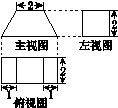
    图K40­15

    　　　

    图K40­16

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设α，β，γ为三个不同的平面，m，n是两条不同的直线，在命题“若α∩β＝m，n⊂γ，且________，则m∥n”中的横线处填入下列三组条件中的一组，使该命题为真命题．

    ①α∥γ，n⊂β；②m∥γ，n∥β；③n∥β，m⊂γ.

    可以填入的条件有________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图K43­2所示，在四面体D ­ ABC中，若AB＝CB，AD＝CD，E是AC的中点，则下列正确的是(　　)

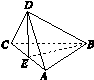
    图K43­2

    A．平面ABC⊥平面ABD

    B．平面ABD⊥平面BDC

    C．平面ABC⊥平面BDE，且平面ADC⊥平面BDE

    D．平面ABC⊥平面ADC，且平面ADC⊥平面BDE

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图K45­9所示，在三棱柱ABC ­ A1B1C1中，AB⊥AC，顶点A1在底面ABC上的射影恰为点B，且AB＝AC＝A1B＝2.

    (1)证明：平面A1AC⊥平面AB1B；

    (2)求棱AA1与BC所成角的大小；

    (3)若点P为B1C1的中点，请求出二面角P ­ AB ­ A1的余弦值．

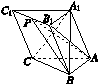
    图K45­9

    查看答案和解析>>

    同步练习册答案