Question

（08年北京卷文）（本小题共13分）

数列满足，（），是常数．

（Ⅰ）当时，求及的值；

（Ⅱ）数列是否可能为等差数列？若可能，求出它的通项公式；若不可能，说明理由；

（Ⅲ）求的取值范围，使得存在正整数，当时总有．

Answer 1

解：（Ⅰ）由于，且．

所以当时，得，故．

从而．

（Ⅱ）数列不可能为等差数列，证明如下：

由，

得，，．

若存在，使为等差数列，则，即，

解得．于是，．

这与为等差数列矛盾．所以，对任意，都不可能是等差数列．

（Ⅲ）记，根据题意可知，且，即

且，这时总存在，满足：当时，；

当时，．

所以由及可知，若为偶数，则，从而当时，；若为奇数，则，从而当时．

因此“存在，当时总有”的充分必要条件是：为偶数，

记，则满足．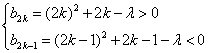

故的取值范围是．

【高考考点】递推数列，等差数列的判定及通项公式；数列与不等式的交汇。

【备考提示】作为压轴题，往往是综合性较强，深难度较高，因此，在解压轴题时，要注意分段得分、分步得分、跳步得分。要学会和敢于取舍。