
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)设![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(1)讨论见解析(2)证明见解析
【解析】
(1)求出函数![]() 的定义域以及函数的导数,然后根据
的定义域以及函数的导数,然后根据![]() 的正负性进行分类讨论,求出函数的单调区间;
的正负性进行分类讨论,求出函数的单调区间;
(2)当![]() 时,求出函数
时,求出函数![]() 的导数,可以确定
的导数,可以确定![]() 的单调性,设
的单调性,设![]() ,可以证明出
,可以证明出![]() ,根据
,根据![]() ,可以证明出
,可以证明出![]() ,根据同角的三角函数关系式可以得到
,根据同角的三角函数关系式可以得到![]() ,最后根据余弦函数的单调性进行证明即可.
,最后根据余弦函数的单调性进行证明即可.
(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,由
时,由![]() 解得
解得![]() ,由
,由![]() 解得
解得![]() ,所以
,所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)当![]() 时,
时,![]() ,
,![]() ,则
,则![]() 在
在![]() 上单调递增.设
上单调递增.设![]() ,且
,且![]() ,则
,则![]() ,即
,即![]() ,所以
,所以![]() ,可得
,可得![]() .因为
.因为![]() ,所以
,所以![]() ,所以
,所以![]() ,即
,即![]() .因为
.因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() .综上可得,
.综上可得,![]() ,且
,且![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】某市据实际情况主要采取以下四种扶贫方式:第一,以工代赈方式,指政府投资建设基础设施工程,组织贫困地区群众参加工程建设并获得劳务报酬,第二,整村推进方式指以贫困村为具体帮扶对象,帮扶对口到村,资金安排到村,扶贫效益到户,第三,科技扶贫方式,指组织科技人员深入贫困乡村实地指导、技术培训等传授科技知识,第四,移民搬迁方式,指对目前极少数居住在生存条件恶劣、自然资源贫乏地区的特困人口,实行自愿移民,该市为了2020年更好的完成精准扶贫各项任务,2020年初在全市贫困户(分一般贫困户和“五特”户两类)中随机抽取了5000户就目前的主要四种扶贫方式行了问卷调查,支持每种扶贫方式的结果如表:
调查的贫困户 | 支持以工代赈户数 | 支持整村推进户数 | 支持科技扶贫户数 | 支持移民搬迁户数 |
一般贫困户 | 1200 | 1600 |
| 200 |
五特户(五保户和特困户) | 100 |
|
| 100 |
已知在被调查的5000户中随机抽取一户支持整村推进的概率为0.36.
(Ⅰ)现用分层抽样的方法在所有参与调查的贫困户中抽取50户进行深入访谈,问应在支持科技扶贫户数中抽取多少户?
(Ⅱ)虽然“五特”户在全市的贫困户所占比例不大,但本次调查要有意义,其中这次调查的“五特”户户数不能低于被调查总户数的9.2%,已知![]() ,求本次调查有意义的概率是多少?
,求本次调查有意义的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》全称《新编直指算法统宗》,是屮国古代数学名著,程大位著.书中有如下问题:“今有五人均银四十两,甲得十两四钱,戊得五两六钱.问:次第均之,乙丙丁各该若干?”意思是:有5人分40两银子,甲分10两4钱,戊分5两6钱,且相邻两项差相等,则乙丙丁各分几两几钱?(注:1两等于10钱)( )
A.乙分8两,丙分8两,丁分8两B.乙分8两2钱,丙分8两,丁分7两8钱
C.乙分9两2钱,丙分8两,丁分6两8钱D.乙分9两,丙分8两,丁分7两
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 中,
中,![]() 是棱
是棱![]() 的中点,
的中点,![]() 是侧面
是侧面![]() 上的动点,且
上的动点,且![]() 平面
平面![]() ,记
,记![]() 与
与![]() 的轨迹构成的平面为
的轨迹构成的平面为![]() .
.
①![]() ,使得
,使得![]() ;
;
②直线![]() 与直线
与直线![]() 所成角的正切值的取值范围是
所成角的正切值的取值范围是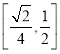 ;
;
③![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ;
;
④正方体![]() 的各个侧面中,与
的各个侧面中,与![]() 所成的锐二面角相等的侧面共四个.
所成的锐二面角相等的侧面共四个.
其中正确命题的序号是________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列![]() 中,已知
中,已知![]() ,
,![]() .设数列
.设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ,
,![]() (
(![]() ,
,![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)是否存在等差数列![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ?若存在,求出所有符合题意的等差数列
?若存在,求出所有符合题意的等差数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com