已知n∈R,函数,f(x)=(-x2+ax)ex(x∈R,e为自然对数的底数).
(1)当a=2时,求函数f(x)的单调递增区间;
(2)若函数f(x)在(-1,1)上单调递增,求a的取值范围;
(3)函数f(x)是否为R上的单调函数?若是,求出a的取值范围;若不是,请说明理由.
【答案】
分析:(1)求导函数,令f′(x)>0,可得f(x)的单调递增区间;
(2)f′(x)=[-x
2+(a-2)x+a]e
x,若f(x)在(-1,1)内单调递增,即当-1<x<1时,f′(x)≥0,即-x
2+(a-2)x+a≥0对x∈(-1,1)恒成立,分离参数求最值,即可求a的取值范围.
(3)假设f(x)是为R上的单调函数,则为R上的单调递增函数或单调递减函数,意即f′(x)≥0或f′(x)≤0对任意的x∈R都成立.可转化为二次不等式恒成立问题.
解答:解:解:(Ⅰ)当a=2时,f(x)=(-x
2+2x)e
x,f′(x)=-(x
2-2)e
x令f′(x)>0,得x
2-2<0,∴
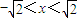
∴f(x)的单调递增区间是(
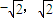
);
(Ⅱ)f′(x)=[-x
2+(a-2)x+a]e
x,若f(x)在(-1,1)内单调递增,即当-1<x<1时,f′(x)≥0,
即-x
2+(a-2)x+a≥0对x∈(-1,1)恒成立,
即a≥

对x∈(-1,1)恒成立,
令y=
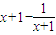
,则y′=
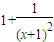
>0
∴y=

在(-1,1)上单调递增,∴y<1+1-
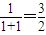
∴a
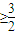
当a=

时,当且仅当x=0时,f′(x)=0
∴a的取值范围是[

,+∞).
(3)假设f(x)是为R上的单调函数,则为R上的单调递增函数或单调递减函数
①若f(x)是R上的单调递减函数,则f′(x)≤0对任意的x∈R都成立,
即[-x
2+(a-2)x+a]e
x≤0对任意的x∈R都成立,
因为e
x>0,所以-x
2+(a-2)x+a≤0恒成立,
故由△=(a-2)2+4a≤0,
整理得a2+4≤0,显然不成立,
即f(x)不可能为R上的单调递减函数.
②若f(x)是R上的单调递增函数,则f′(x)≥0对任意的x∈R都成立,
即[-x
2+(a-2)x+a]e
x≥0对任意的x∈R都成立,
因为e
x>0,所以-x
2+(a-2)x+a≥0恒成立,
而函数h(x)=-x
2+(a-2)x+a的图象是开口向下的抛物线,
所以-x
2+(a-2)x+a≥0是不能恒成立的,
所以f(x)不可能为R上的单调递增函数.
综上所述,f(x)是不可能为R上的单调函数.
点评:本题考查导数知识的运用,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

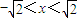
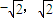 );
); 对x∈(-1,1)恒成立,
对x∈(-1,1)恒成立,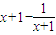 ,则y′=
,则y′=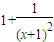 >0
>0 在(-1,1)上单调递增,∴y<1+1-
在(-1,1)上单调递增,∴y<1+1-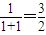
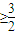
 时,当且仅当x=0时,f′(x)=0
时,当且仅当x=0时,f′(x)=0 ,+∞).
,+∞).

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案