
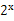 -2,若同时满足条件:
-2,若同时满足条件: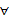 x∈R,f(x) <0或g(x) <0;②
x∈R,f(x) <0或g(x) <0;②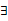 x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。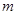 的取值范围为
的取值范围为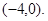
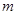 的取值范围为
的取值范围为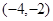
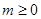 时不能保证对
时不能保证对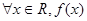 <0或
<0或 <0成立.
<0成立.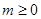 时不能保证对
时不能保证对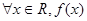 <0或
<0或 <0成立.
<0成立.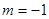 时,
时,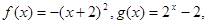 此时显然满足条件①;
此时显然满足条件①;
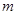 <0时,
<0时,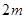 >
>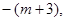 要使其满足条件①,则需-1<
要使其满足条件①,则需-1<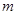 <0且
<0且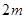 <1,解得-1<
<1,解得-1<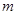 <0;
<0; 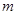 <-1时,
<-1时, >
>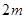 ,要使其满足条件①,则需
,要使其满足条件①,则需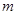 <-1且
<-1且 <1,
<1,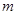 <-1. 因此满足条件①的
<-1. 因此满足条件①的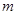 的取值范围为
的取值范围为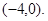
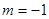 时,在
时,在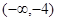 上,
上,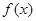 与
与 均小于0,不合题意;
均小于0,不合题意;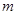 <-1时,则需
<-1时,则需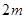 <-4,即
<-4,即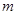 <-2,所以-4<
<-2,所以-4<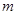 <-2.
<-2.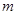 <0时,则需
<0时,则需 <-4,即
<-4,即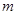 >1,此时无解。
>1,此时无解。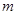 的取值范围为
的取值范围为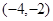


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com