解:(1)由
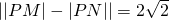
,知点P的轨迹是以M(-2,0),N(2,0)为焦点,
实轴长为

的双曲线.(2分)
即设
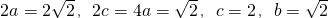
所以所求的W的方程为x
2-y
2=2(4分)
(2)若k不存在,即x=2时,可得A(2,

),B(2,-

),|AB|=2

满足题意;(5分)
若k存在,可设l:y=k(x-2)
联立
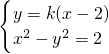
,?(1-k
2)x
2+4k
2x-4k
2-2=0
由题意知
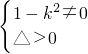
?k∈R且k≠±1(6分)
设A(x
1,y
1),B(x
2,y
2),则|AB|=
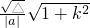
即
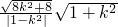
=2

?k=0即l:y=0(8分)
所以直线l的方程为x=2或y=0(9分)
(3)
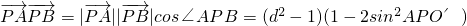
=
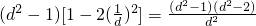
;
又d
2=x
2+(y-4)
2=y
2+2+(y-4)
2=2y
2-8y+18=2(y-2)
2+10≥10
则

=
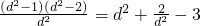
∵d
2≥10(13分)
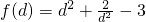
在
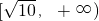
是增函数,
∴
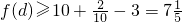
则所求的

的范围为

(16分)
分析:(1)由
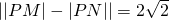
,知点P的轨迹是以M(-2,0),N(2,0)为焦点,实轴长为

的双曲线.由此能求出W的方程.
(2)若k不存在,即x=2时,可得A(2,

),B(2,-

),|AB|=2

满足题意;若k存在,可设l:y=k(x-2),联立
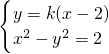
,得(1-k
2)x
2+4k
2x-4k
2-2=0.由题意知
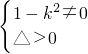
,k≠±1.设A(x
1,y
1),B(x
2,y
2),则|AB|=
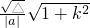
.由此能求出直线l的方程.
(3)
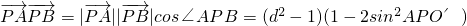
=
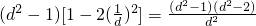
,由d
2=x
2+(y-4)
2=y
2+2+(y-4)
2=2y
2-8y+18=2(y-2)
2+10≥10,知

=
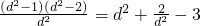
,由此能求出

的范围.
点评:本题考查双曲线方程和直线方程的求法,求

的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用圆锥曲线的性质和向量数量积计算公式,合理地进行等价转化.

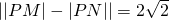 ,记动点P的轨迹为W.
,记动点P的轨迹为W. ,求直线l的方程.
,求直线l的方程. ,并求
,并求 的取值范围.
的取值范围.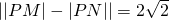 ,知点P的轨迹是以M(-2,0),N(2,0)为焦点,
,知点P的轨迹是以M(-2,0),N(2,0)为焦点, 的双曲线.(2分)
的双曲线.(2分)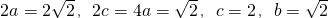
 ),B(2,-
),B(2,- ),|AB|=2
),|AB|=2 满足题意;(5分)
满足题意;(5分)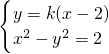 ,?(1-k2)x2+4k2x-4k2-2=0
,?(1-k2)x2+4k2x-4k2-2=0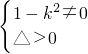 ?k∈R且k≠±1(6分)
?k∈R且k≠±1(6分)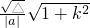
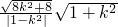 =2
=2 ?k=0即l:y=0(8分)
?k=0即l:y=0(8分)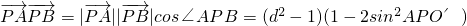 =
=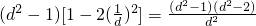 ;
; =
=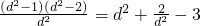
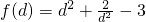 在
在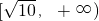 是增函数,
是增函数,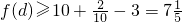
 的范围为
的范围为 (16分)
(16分)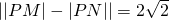 ,知点P的轨迹是以M(-2,0),N(2,0)为焦点,实轴长为
,知点P的轨迹是以M(-2,0),N(2,0)为焦点,实轴长为 的双曲线.由此能求出W的方程.
的双曲线.由此能求出W的方程. ),B(2,-
),B(2,- ),|AB|=2
),|AB|=2 满足题意;若k存在,可设l:y=k(x-2),联立
满足题意;若k存在,可设l:y=k(x-2),联立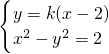 ,得(1-k2)x2+4k2x-4k2-2=0.由题意知
,得(1-k2)x2+4k2x-4k2-2=0.由题意知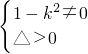 ,k≠±1.设A(x1,y1),B(x2,y2),则|AB|=
,k≠±1.设A(x1,y1),B(x2,y2),则|AB|=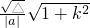 .由此能求出直线l的方程.
.由此能求出直线l的方程.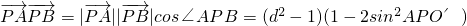 =
=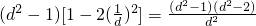 ,由d2=x2+(y-4)2=y2+2+(y-4)2=2y2-8y+18=2(y-2)2+10≥10,知
,由d2=x2+(y-4)2=y2+2+(y-4)2=2y2-8y+18=2(y-2)2+10≥10,知 =
=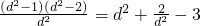 ,由此能求出
,由此能求出 的范围.
的范围. 的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用圆锥曲线的性质和向量数量积计算公式,合理地进行等价转化.
的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用圆锥曲线的性质和向量数量积计算公式,合理地进行等价转化. 

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案