分析:分a<2,a>3,2<a<3三种情况进行讨论:根据图象的特殊点可作出函数图象,根据图象及函数单调性可表示出
f(t1)=,
f(t2)=,由此可得t
1-t
2的取值范围.
解答: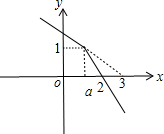
解:(1)当a<2时,作出f(x)的图象如图所示:
由图象知,
f(t1)=可化为
=
,得
t1=(a-2)+2=
a+1,
f(t2)=可化为
=,得t
2=
(a-3)+3=
a-,
∴t
1-t
2=(
a+1)-(
a-)=-2a+
,
又a<2,∴-2a>-4,∴-2a+
>-4+
=
,即t
1-t
2>
;
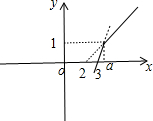
(2)当a>3时,作出f(x)的图象如图所示:
由图象知,
=,得
t1=(a-3)+3=
a+
,
f(t2)=可化为5
=,得
t2=(a-2)+2=
a-3,
∴t
1-t
2=(
a+
)-(
a-3)=-2a+
,
又a>3,∴-2a<-6,-2a+
<-
,即t
1-t
2<-
;
(3)当2<a<3时,
若x≥a,则
•(x-2)≥
•(a-2)=1;若x<a,则
•(x-3)>
•(a-3)=1,
与
f(t1)=不符,此种情况不可能;
综上所述,t
1-t
2的取值范围是:(
,+∞)∪(-∞,-
).
故答案为:(
,+∞)∪(-∞,-
).
点评:本题考查一次函数的求值问题,考查分类讨论思想、数形结合思想,思维含量较高,正确画出函数图象是解决问题的关键.

 解:(1)当a<2时,作出f(x)的图象如图所示:
解:(1)当a<2时,作出f(x)的图象如图所示: 又a>3,∴-2a<-6,-2a+
又a>3,∴-2a<-6,-2a+

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案