
已知(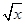 -
-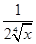 )n的展开式中,前三项系数的绝对值依次成等差数列.(1)证明:展开式中没有常数项;
)n的展开式中,前三项系数的绝对值依次成等差数列.(1)证明:展开式中没有常数项;
(2)求展开式中所有有理项.
(1)见解析 (2) T1=x4,T5= x,T9=
x,T9=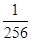 x-2.
x-2.
【解析】(1)本小题利用展开式的通项,只要说明x的系数不可能等于零即可.在具体证明时可采用反证法.
(2)根据展开式的通项公式,让x的系数为整数,看有哪些项即可
依题意,前三项系数的绝对值是1,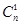 (
(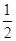 ),
),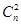 (
(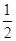 )2,
)2,
且2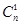 ·
·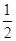 =1+
=1+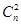 (
(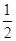 )2,即n2-9n+8=0,∴n=8(n=1舍去),
)2,即n2-9n+8=0,∴n=8(n=1舍去),
∴展开式的第k+1项为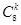 (
(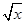 )8-k(-
)8-k(-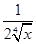 )k
)k
=(-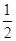 )k
)k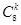 ·x
·x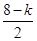 ·x-
·x- =(-1)k·
=(-1)k·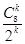 ·x
·x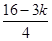 .
.
(1)证明:若第k+1项为常数项,
当且仅当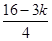 =0,即3k=16,∵k∈Z,∴这不可能,∴展开式中没有常数项.
=0,即3k=16,∵k∈Z,∴这不可能,∴展开式中没有常数项.
(2)若第k+1项为有理项,当且仅当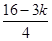 为整数,∵0≤k≤8,k∈Z,∴k=0,4,8,
为整数,∵0≤k≤8,k∈Z,∴k=0,4,8,
即展开式中的有理项共有三项,它们是:T1=x4,T5= x,T9=
x,T9=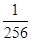 x-2.
x-2.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
| 3 | x |
| 1 | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 2 | |||
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com