分析:(I)由题意,由于可证得CD⊥平面A1ABB1.故点C到平面的距离即为CD的长度,易求;
(II)解法一:由题意结合图象,可通过作辅助线先作出二面角的平面角∠A1DD1,然后在直角三角形A1D1D中求出二面角的余弦;
解法二:根据几何体的形状,可过D作DD1∥AA1交A1B1于D1,在直三棱柱中,可得DB,DC,DD1两两垂直,则以D为原点,射线DB,DC,DD1分别为X轴、Y轴、Z轴的正半轴建立空间直角坐标系D-xyz.给出各点的坐标,分别求出两平面的法向量,求出两向量的夹角即为两平面的夹角.
解答: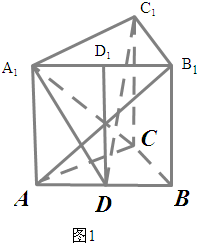
解:(I)由AC=BC,D为AB的中点,得CD⊥AB.又CD⊥AA
1.
故CD⊥平面A
1ABB
1.
所以点C到平面A
1ABB
1的距离为CD=
=
(II)解法一:如图1,取D
1为A
1B
1的中点,连接DD
1,则DD
1∥AA
1∥CC
1.
又由(I)知CD⊥平面A
1ABB
1.故CD⊥A
1D,CD⊥D
1D,所以∠A
1DD
1为所求的二面角A
1-CD-C
1的平面角.因A
1D为A
1C在面A
1ABB
1中的射影,又已知AB
1⊥A
1C由三垂线定理的逆定理得AB
1⊥A
1D.从而∠A
1AB
1、∠A
1DA都与∠B
1AB互余.因此∠A
1AB
1=∠A
1DA,所以Rt△A
1AD∽Rt△B
1A
1A.因此AA
1:AD=A
1B
1:AA
1,即AA
12=AD•A
1B
1=8,得AA
1=2
,从而A
1D=
=2
.所以Rt△A
1D
1D中,cos∠A
1DD
1=
=
=
解法二:如图2,过D作DD
1∥AA
1交A
1B
1于D
1,在直三棱柱中,有DB,DC,DD
1两两垂直,以D为原点,射线DB,DC,DD
1分别为X轴、Y轴、Z轴的正半轴建立空间直角坐标系D-xyz.
设直三棱柱的高为h,则A(-2,0,0),A
1(-2,0,h),B
1(2,0,h),C(0,
,0),C
1(0,
,h),从而
=(4,0,h),
=(2,
,-h)
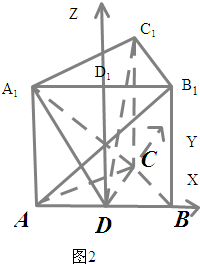
由AB
1⊥A
1C,可得8-h
2=0,h=2
,故
=(-2,0,2),
=(0,0,2
),
=(0,
,0)
设平面A
1CD的法向量为
=(x
1,y
1,z
1),则有
⊥
,
⊥
∴
•
=0且
•
=0,即
,取z
1=1,则
=(
,0,1)
设平面C
1CD的法向量为
=(x
2,y
2,z
2),则
⊥
,
⊥
,即
y2=0且
2z2=0,取x
2=1,得
=(1,0,0),
所以cos<
,
>=
=
=
,所以二面角A
1-CD-C
1的平面角的余弦值
点评:本题考查二面角的求法及点到面距离的求法,点到面的求法一般是作垂线,垂线段的长度即所求,二面角的余弦值的求法有两种,一种是几何法,找到二面角平面角所在的三角形,解三角形求出角的余弦值,第二种方法是现在比较常用的方法向量法,其特征是思维量小,计算量大,作题时对这两种方法要根据题设灵活选用

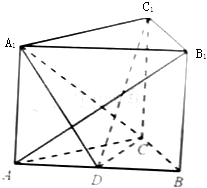 (2012•重庆)如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点
(2012•重庆)如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点 解:(I)由AC=BC,D为AB的中点,得CD⊥AB.又CD⊥AA1.
解:(I)由AC=BC,D为AB的中点,得CD⊥AB.又CD⊥AA1.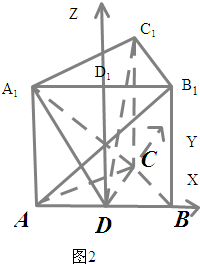


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (2012•重庆)如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.
(2012•重庆)如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形. (2012•重庆)如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.
(2012•重庆)如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形. (2012•重庆)如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点.
(2012•重庆)如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点.