
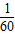 ,固定部分为60元.
,固定部分为60元.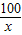 小时;汽车每小时的运输成本的可变部分为
小时;汽车每小时的运输成本的可变部分为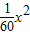 元;汽车每小时的全部运输成本为(
元;汽车每小时的全部运输成本为(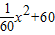 )元;
)元;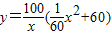 ,即
,即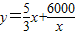 (0<x≤60).
(0<x≤60).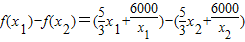
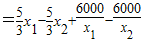 =
= (x1-x2)(
(x1-x2)(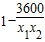 )
)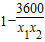 <0,
<0,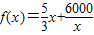 在(0,60]上是减函数.
在(0,60]上是减函数.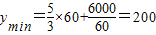 .
.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| v |
| 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年江西省高一上学期第一次阶段考试数学卷 题型:选择题
新余市乘出租车计费规定:2公里以内5元,超过2公里不超过8公里按每公
里1.6元计费,超过8公里以后按每公里2.4元计费。若甲、乙两地相距10公里,则乘出
租车从甲地到乙地共需要支付乘车费为 ( )
A 19.4元 B 20.4元 C 21.8元 D 22.8元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com