
分析 由条件利用向量的数乘,两个向量的数量积的运算,正弦函数的图象和性质,逐一判断各个选项是否正确,从而得出结论.
解答 解:∵0•$\vec a$=$\overrightarrow{0}$,故①不正确;
∵函数y=sin($\frac{3}{2}$π+x)=-cosx 是偶函数,故②正确;
若$\vec a$•$\vec b$=0,则有可能$\overrightarrow{a}$=$\overrightarrow{0}$,不一定$\vec a$⊥$\vec b$,故③不正确;
当x=$\frac{π}{8}$时,函数y=sin(2x+$\frac{5}{4}$π)=-1,为最小值,故x=$\frac{π}{8}$是函数y=sin(2x+$\frac{5}{4}$π)的一条对称轴方程,故④正确;
若α、β是第一象限的角,且α>β,则sinα>sinβ不一定成立,如α=30°,β=-300°时,sinα=$\frac{1}{2}$,sinβ=$\frac{\sqrt{3}}{2}$,故⑤不正确;
由于函数f(x)=sinx+cos2x=-sin2x+sinx+1=-${(sinx-\frac{1}{2})}^{2}$+$\frac{5}{4}$,故当sinx=$\frac{1}{2}$时,函数取得最大值为$\frac{5}{4}$,故⑥正确.
综上可得,只有②④⑥正确,
故答案为:②④⑥.
点评 本题主要考查命题的真假的判断,向量的数乘,两个向量的数量积的运算,正弦函数的图象和性质,属于中档题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0,则x≠0或y≠0” | |
| B. | 若命题p为假命题,命题¬q为真命题,则命题“p∨q”为真命题 | |
| C. | “$\frac{a}{b}$>1”是“a>b>0”的必要不充分条件 | |
| D. | 命题“任意x>1,x+1>2”的否定是“存在x≤1,x+1≤2” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
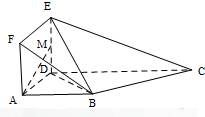 如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.
如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com