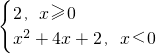练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f（x）=数学公式的图象与直线y=k（x+2）-2恰有三个公共点，则实数k的取值范围是


    1. A.
      （0，2）
    2. B.
      （0，2]
    3. C.
      （-∞，2）
    4. D.
      （2，+∞）
    A
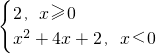    分析：首先根据函数的表达式f（x）=画出函数的图象，从而根据图象判断函数与直线的公共点的情况，最后结合两曲线相切与图象恰有三个不同的公共点的关系即可求得实数k的取值范围．
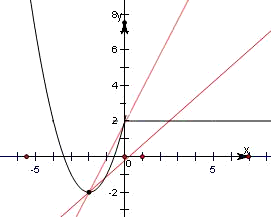    解答：解：画出函数f（x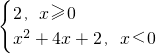）=，（如图）．
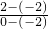    由图可知，当恒过抛物线的项点（-2，-2）的直线y=k（x+2）-2与函数的图象相切时，即直线y=k（x+2）-2的斜率k=0时，恰有一个公共点；
    当直线y=k（x+2）-2过（0，2）时，k==2时，恰有二个公共点．
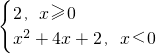    故函数f（x）=的图象与直线y=k（x+2）-2恰有三个公共点，则实数k的取值范围是0＜k＜2．
    故选A．
    点评：本题主要考查函数的图象的交点以及数形结合方法，数形结合是数学解题中常用的思想方法，本题由于使用了数形结合的方法，使得问题便迎刃而解，且解法简捷．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    4、已知函数f（x）=2x的反函数为f-1（x），则f-1（x）＜0的解集是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=x3的切线的斜率等于1，则这样的切线有（　　）
    A、1条B、2条C、3条D、不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=|sinx|的图象与直线y=kx（k＞0）有且仅有三个交点，交点的横坐标的最大值为α，求证：
    cosα
    sinα+sin3α
    =
    1+α2
    4α
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=-x2的图象在P（a，-a2）（a≠0）处的切线与两坐标轴所围成的三角形的面积为2，则实数a的值为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=2x的图象与函数g（x）的图象关于直线y=x对称，令h（x）=g（1-|x|）则关于函数h（x）有下列命题：
    ①h（x）为图象关于y轴对称；
    ②h（x）是奇函数；
    ③h（x）的最小值为0；
    ④h（x）在（0，1）上为减函数．
    其中正确命题的序号为
    ①④
    ①④
    （注：将所有正确命题的序号都填上）．

    查看答案和解析>>

    同步练习册答案