
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
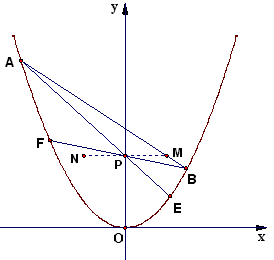
 (2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….
(2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:013
已知抛物线y2=x+4上一点A(0,2)和两个动点P、Q,当PQ^PA时,点Q的纵坐标取值范围是( )
A.[-¥,0] B.[4,+¥) C.[0,4] D.(-¥,0]∪[4,+¥)
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
A.[-¥,0] B.[4,+¥) C.[0,4] D.(-¥,0]∪[4,+¥)
查看答案和解析>>
科目:高中数学 来源:2012年北京市西城区高考数学一模试卷(文科)(解析版) 题型:解答题
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com