
【题目】已知m,n为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( )
A.mα,nα,m∥β,n∥βα∥β
B.α∥β,mα,nβ,m∥n
C.m⊥α,m⊥nn∥α
D.m∥n,n⊥αm⊥α
【答案】D
【解析】解:在长方体ABCD﹣A1B1C1D1中, A、若平面AC是平面α,平面BC1是平面β,
直线AD是直线m,点E,F分别是AB,CD的中点,则EF∥AD,EF是直线n,
显然满足α∥β,mα,nβ,但是m与n异面;
B、若平面AC是平面α,平面A1C1是平面β,
直线AD是直线m,A1B1是直线n,
显然满足mα,nα,m∥β,n∥β,但是α与β相交;
C、若平面AC是平面α,直线AD是直线n,AA1是直线m,
显然满足m⊥α,m⊥n,但是n∈α;
故选D.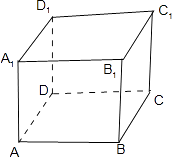
根据m,n为两条不同的直线,α,β为两个不同的平面,可得该直线与直线可以平行,相交或异面,平面与平面平行或相交,把平面和直线放在长方体中,逐个排除易寻到答案.


 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:
【题目】设min{m,n}表示m、n二者中较小的一个,已知函数f(x)=x2+8x+14,g(x)=min{( ![]() )x﹣2 , log2(4x)}(x>0),若x1∈[﹣5,a](a≥﹣4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为( )
)x﹣2 , log2(4x)}(x>0),若x1∈[﹣5,a](a≥﹣4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为( )
A.﹣4
B.﹣3
C.﹣2
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos2x+2 ![]() sinxcosx+a,且当x∈[0,
sinxcosx+a,且当x∈[0, ![]() ]时,f(x)的最小值为2.
]时,f(x)的最小值为2.
(1)求a的值,并求f(x)的单调递增区间;
(2)先将函数y=f(x)的图象上的点纵坐标不变,横坐标缩小到原来的 ![]() ,再将所得图象向右平移
,再将所得图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,求方程g(x)=4在区间[0,
个单位,得到函数y=g(x)的图象,求方程g(x)=4在区间[0, ![]() ]上所有根之和.
]上所有根之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二阶矩阵M有特征值λ=8及对应的一个特征向量 ![]() =[
=[ ![]() ],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项为a1 , 公差为d,其前n项和为Sn , 若直线y=a1x+m与圆x2+(y﹣1)2=1的两个交点关于直线x+y﹣d=0对称,则数列( ![]() )的前100项的和为 .
)的前100项的和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的方程为x+y+3=0,以直角坐标系中x轴的正半轴为极轴的极坐标系中,圆M的极坐标方程为ρ=2sinθ. (Ⅰ)写出圆M的直角坐标方程及过点P(2,0)且平行于l的直线l1的参数方程;
(Ⅱ)设l1与圆M的两个交点为A,B,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,曲线C1的参数方程为 ![]() (θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,与直角坐标系xoy取相同的单位长度建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ﹣4sinθ.
(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,与直角坐标系xoy取相同的单位长度建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ﹣4sinθ.
(1)化曲线C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(2)设曲线C2与x轴的一个交点的坐标为P(m,0)(m>0),经过点P作斜率为1的直线,l交曲线C2于A,B两点,求线段AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com