
(08年湖南卷理)(本小题满分12分)
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,
E是CD的中点,PA⊥底面ABCD,PA=2.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的大小.
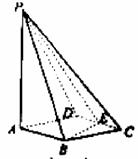
解: 解法一(Ⅰ)如图所示,连结BD,由ABCD是菱形且∠BCD=60°知,
△BCD是等边三角形.因为E是CD的中点,所以BE⊥CD,又AB∥CD,
所以BE⊥AB.又因为PA⊥平面ABCD,![]() 平面ABCD,所以
平面ABCD,所以
PA⊥BE.而![]() AB=A,因此BE⊥平面PAB.
AB=A,因此BE⊥平面PAB.
又![]() 平面PBE,所以平面PBE⊥平面PAB.
平面PBE,所以平面PBE⊥平面PAB.
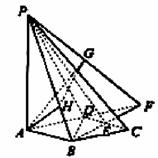
(Ⅱ)延长AD、BE相交于点F,连结PF.
过点A作AH⊥PB于H,由(Ⅰ)知
平面PBE⊥平面PAB,所以AH⊥平面PBE.
在Rt△ABF中,因为∠BAF=60°,
所以,AF=2AB=2=AP.
在等腰Rt△PAF中,取PF的中点G,连接AG.
则AG⊥PF.连结HG,由三垂线定理的逆定理得,
PF⊥HG.所以∠AGH是平面PAD和平面PBE所成二面角的平面角(锐角).
在等腰Rt△PAF中, ![]()
在Rt△PAB中, ![]()
所以,在Rt△AHG中, 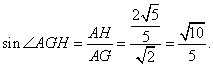
故平面PAD和平面PBE所成二面角(锐角)的大小是![]()
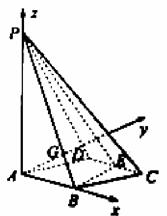
解法二: 如图所示,以A为原点,建立空间直角坐标系.则相关
各点的坐标分别是A(0,0,0),B(1,0,0),
![]()
![]() P(0,0,2),
P(0,0,2),![]()
(Ⅰ)因为![]() ,
,
平面PAB的一个法向量是![]() ,
,
所以![]() 共线.从而BE⊥平面PAB.
共线.从而BE⊥平面PAB.
又因为![]() 平面PBE,
平面PBE,
故平面PBE⊥平面PAB.
(Ⅱ)易知![]()
![]()
设![]() 是平面PBE的一个法向量,则由
是平面PBE的一个法向量,则由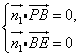 得
得
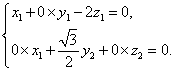 所以
所以![]()
设![]() 是平面PAD的一个法向量,则由
是平面PAD的一个法向量,则由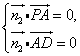 得
得
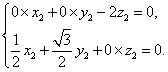 所以
所以![]() 故可取
故可取![]()
于是,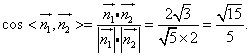
故平面PAD和平面PBE所成二面角(锐角)的大小是![]()


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com