
已知函数f(x)=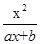 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式f(x)< 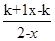 .
.
(1)f(x)=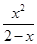 (x≠2)
(x≠2)
(2)当1<k<2时,原不等式的解集为{x|1<x<k或x>2};
当k=2时,原不等式的解集为{x|x>1且x≠2};
当k>2时,原不等式的解集为{x|1<x<2或x>k}.
解析试题分析:解: (1)将x1=3,x2=4分别代入方程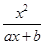 -x+12=0,得
-x+12=0,得 , 3分
, 3分
解得 .
.
∴f(x)=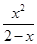 (x≠2) 5分
(x≠2) 5分
(2)原不等式即为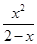 <
<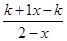 ,可化为
,可化为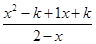 <0. 6分
<0. 6分
即(x-2)(x-1)(x-k)>0. 7分
①当1<k<2时,1<x<k或x>2; 9分
②当k=2时,x>1且x≠2; 10分
③当k>2时,1<x<2或x>k. 12分
综上所述,当1<k<2时,原不等式的解集为{x|1<x<k或x>2};
当k=2时,原不等式的解集为{x|x>1且x≠2};
当k>2时,原不等式的解集为{x|1<x<2或x>k}. 13分
考点:函数解析式,一元二次不等式
点评:主要是考查了函数解析式以及一元二次不等式的求解,体现了分类讨论思想的运用,属于中档题。


科目:高中数学 来源: 题型:解答题
某面包厂2011年利润为100万元,因市场竞争,若不开发新项目,预测从2012年起每年利润比上一年减少4万元.2012年初,该面包厂一次性投入90万元开发新项目,预测在未扣除开发所投入资金的情况下,第 年(
年( 为正整数,2012年为第一年)的利润为
为正整数,2012年为第一年)的利润为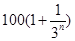 万元.设从2012年起的前
万元.设从2012年起的前 年,该厂不开发新项目的累计利润为
年,该厂不开发新项目的累计利润为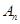 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为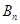 万元(须扣除开发所投入资金).
万元(须扣除开发所投入资金).
(1)求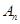 ,
,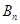 的表达式;
的表达式;
(2)问该新项目的开发是否有效(即开发新项目的累计利润超过不开发新项目的累计利润),如果有效,从第几年开始有效;如果无效,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)
(1)试将 表示为
表示为 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器。已知喷水器的喷水区域是半径为5m的圆。问如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com