Question

14．如图，在底面是边长为4的等边三角形的直三棱柱ABO-A₁B₁O₁中，|AA₁|=6，D为A₁B₁的中点，
（1）A₁的坐标是（2$\sqrt{3}$，2，0）；
（2）$\overrightarrow{OD}$的坐标是（$\sqrt{3}$，3，6）；
（3）直线OD与面O₁OAA₁所成角是arcsin$\frac{1}{4}$．

Answer 1

分析 （1）直接利用正三棱柱求解即可相关点坐标，（2）直接求解向量．（3）利用斜率的数量积求解直线与平面所成角即可．

解答 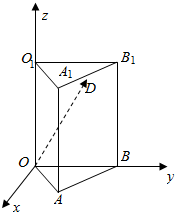解：底面是边长为4的等边三角形的直三棱柱ABO-A₁B₁O₁中，|AA₁|=6，D为A₁B₁的中点，
（1）A₁的坐标是：（2$\sqrt{3}$，2，0）；
（2）D（$\sqrt{3}$，3，6），$\overrightarrow{OD}$的坐标是：（$\sqrt{3}$，3，6）；
（3）$\overrightarrow{OD}$=（$\sqrt{3}$，3，6）；
平面O₁OAA₁的一个法向量为：（$\sqrt{3}$，-3，0）．
直线OD与面O₁OAA₁所成角是θ．
sinθ=$\left|\frac{\overrightarrow{n}•\overrightarrow{OD}}{\left|\overrightarrow{n}\right|•\left|\overrightarrow{OD}\right|}\right|$=$\left|\frac{3-9}{\sqrt{3+9}•\sqrt{3+9+36}}\right|$=$\frac{6}{12×2}$=$\frac{1}{4}$．
θ=arcsin$\frac{1}{4}$．
故答案为：（1）（2$\sqrt{3}$，2，0）；
（2）：（$\sqrt{3}$，3，6）；
（3）：arcsin$\frac{1}{4}$．

点评 本题考查空间向量的应用，直线与平面所成角的求法，考查转化思想以及计算能力．