
(2005
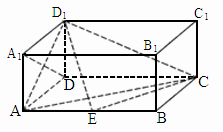
江西,20)如下图,在长方体 中,
中, ,AB=2,点E在棱AB上移动.
,AB=2,点E在棱AB上移动.
(1)
证明: ;
;
(2)
当E为AB的中点时,求点E到面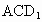 的距离;
的距离;
(3)AE
等于何值时,二面角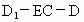 的大小为
的大小为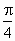 .
. |
解析:解法一: (1)∵AE⊥平面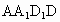 , ,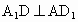 , ,
∴ 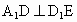 . .
(2) 设点E到面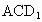 的距离为h,在△ 的距离为h,在△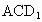 中, 中,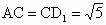 , ,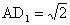 .故 .故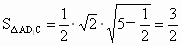 , ,
而  , ,
∴ 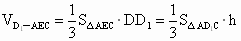 , ,
∴ 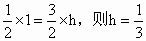 . .
(3) 过D作DH⊥CE于H,连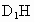 、DE,则 、DE,则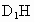 ⊥CE, ⊥CE,
∴  为二面角 为二面角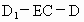 的平面角. 的平面角.
设 AE=x,则BE=2-x,在Rt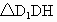 中, 中,
由 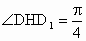 ,得DH=1.∵在Rt△ADE中, ,得DH=1.∵在Rt△ADE中,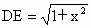 , ,
∴在 Rt△DHE中,EH=x,在Rt△DHC中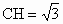 , ,
在 Rt△CBE中,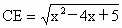 , ,
∴ 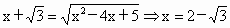 . .
所以 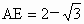 时,二面角 时,二面角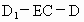 的大小为 的大小为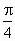 . .
解法二:以 D为坐标原点,直线DA,DC, 分别为x,y,z轴,建立空间直角坐标系,设AE=x,则 分别为x,y,z轴,建立空间直角坐标系,设AE=x,则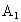 (1,0,1), (1,0,1),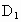 (0,0,1),E(1,x,0),A(1,0,0),C(0,2,0). (0,0,1),E(1,x,0),A(1,0,0),C(0,2,0).
(1) 因为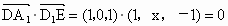 , ,
所以 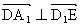 . .
(2) 因为E为AB的中点,则E(1,1,0),从而  , ,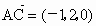 , ,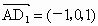 , ,
设平面 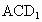 的法向量为n=(a,b,c), 的法向量为n=(a,b,c),
则 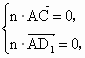 也即 也即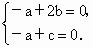 得 得
从而 n=(2,1,2),所以点 E到平面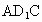 的距离为 的距离为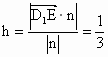 . .
(3) 设平面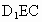 的法向量n=(a,b,c), 的法向量n=(a,b,c),
所以 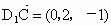 , ,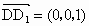 , ,
由 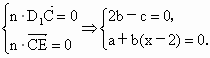
令 b=1,所以c=2,a=2-x.所以n=(2-x,1,2).依题意 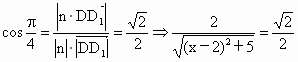 . .
所以  (不合,舍去), (不合,舍去), , ,
所以 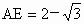 时,二面角 时,二面角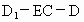 的大小为 的大小为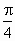 . . |
|
剖析:本题考查线线垂直、点面距离以及二面角的知识,可采用传统综合法或平面向量法求解. |


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com