
如图所示,扇形所含的中心角为90°,弦AB将扇形分成两个部分,这两部分各以AO为轴旋转一周,所得的旋转体体积V1和V2之比为________.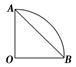
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.
如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.查看答案和解析>>
科目:高中数学 来源:2012年江苏省高考数学压轴卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三高考压轴数学试卷(解析版) 题型:解答题
如图所示,某市政府决定在以政府大楼 为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径
为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径 ,
, ,
,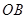 与
与 之间的夹角为
之间的夹角为 .
.

(1)将图书馆底面矩形 的面积
的面积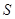 表示成
表示成 的函数.
的函数.
(2)求当 为何值时,矩形
为何值时,矩形 的面积
的面积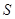 有最大值?
有最大值?
(3)其最大值是多少?(用含R的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com