
 }满足
}满足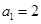 ,且点
,且点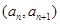 在函数
在函数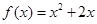 的图象上,其中
的图象上,其中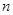 =1,2,3,….
=1,2,3,…. )}是等比数列;
)}是等比数列;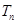 =(1+
=(1+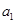 )(1+
)(1+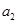 )…(1+
)…(1+ ),求
),求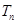 及数列{
及数列{ }的通项.
}的通项.  +1)=2n-1lg(1+
+1)=2n-1lg(1+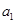 )
)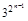 .∴
.∴ +1=
+1=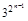 . 则
. 则  =
= 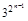 -1
-1 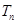 =(1+
=(1+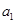 )(1+
)(1+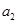 )…(1+
)…(1+ )=
)=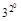 ·
·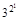 ·
·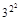 ·…·
·…·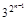
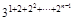 =
=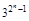 .∴
.∴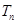 =
=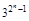 ,
, =
=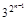 -1.
-1.  ,
,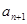 )在函数
)在函数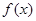 的图象上,
的图象上,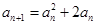 ,从而可得
,从而可得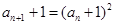 ,
,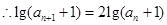 ,从而得到证明.
,从而得到证明.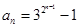 ,然后可知
,然后可知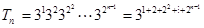 然后再利用等比数列前n项和公式求解.
然后再利用等比数列前n项和公式求解. ,
,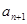 )在函数
)在函数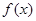 的图象上,
的图象上, 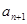 =
= +2
+2 ,∴
,∴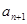 +1=
+1=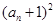 . …………4分
. …………4分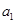 =2,∴
=2,∴ +1﹥1,∴lg(
+1﹥1,∴lg(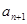 +1)=2lg(
+1)=2lg( +1).
+1). +1)}是公比为2的等比数列. …………6分
+1)}是公比为2的等比数列. …………6分 +1)=2n-1lg(1+
+1)=2n-1lg(1+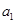 )
)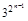 .∴
.∴ +1=
+1=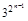 . 则
. 则  =
= 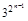 -1 …………9分
-1 …………9分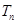 =(1+
=(1+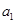 )(1+
)(1+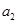 )…(1+
)…(1+ )=
)=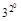 ·
·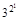 ·
·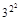 ·…·
·…·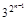
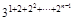 =
=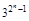 .∴
.∴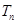 =
=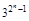 ,
, =
=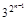 -1. …………12分
-1. …………12分

 53随堂测系列答案
53随堂测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com