练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知|a|＝，|b|＝4，m＝a＋b，n＝a＋λb，〈a，b〉＝135°，m⊥n，则λ＝_________．

    答案：
    解析：

    　　答案：－

    　　解析：由m⊥n，得(a＋b)·(a＋λb)＝0，

    　　a2＋λa·b＋a·b＋λb2＝0，

    　　18＋λ××4×cos135°＋×4×cos135°＋16λ＝0，

    　　4λ＋6＝0，λ＝－．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2012年人教A版高中数学必修四2.4平面向量的数量积练习卷（一）（解析版） 题型：解答题

    已知|a|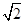＝，|b|＝3，a与b夹角为45°，求使a＋λb与λa＋b的夹角为钝角时，λ的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2012届度辽宁省沈阳市高三数学质量检测试卷 题型：选择题

    已知a＝，b＝，c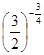＝，则a、b、c的大小关系是  (　　)

     

     

    A．c<a<b            B．a<b<c        C．b<a<c          D．c<b<a

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）已知P＝，S＝，,求实数的取值范围；

    （2）已知A＝，B＝，AB=B,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知|a|＝2|b|，且|b|≠0，关于x的方程x2＋|a|x－a·b＝0有两相等实根，则向量a与b的夹角是(　　)

    (A)－  (B)－  (C)  (D)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知|a|＝2|b|，且|b|≠0，关于x的方程x2＋|a|x－a·b＝0有两相等实根，则向量a与b的夹角是(　　)

    (A)－  (B)－  (C)  (D)

    查看答案和解析>>

    同步练习册答案