
设a为实数,记函数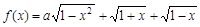 的最大值为
的最大值为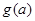 .
.
(1)设t=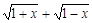 ,求t的取值范围,并把f(x)表示为t的函数m(t) ;
,求t的取值范围,并把f(x)表示为t的函数m(t) ;
(2)求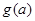 ;
;
(3)试求满足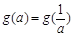 的所有实数a.
的所有实数a.
(1)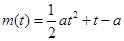 ,
,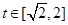 ;(2)
;(2)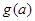 =
=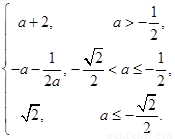 (3)
(3)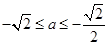 .
.
【解析】
试题分析:(1)根据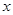 的取值范围求出
的取值范围求出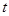 的范围,再将
的范围,再将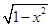 用含
用含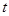 的式子表示;(2)由题意知
的式子表示;(2)由题意知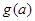 即为函数
即为函数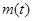
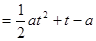 ,
,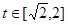 的最大值,因为对称轴含有参数
的最大值,因为对称轴含有参数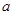 ,所以要讨论处理;(3)根据(2)问得出的
,所以要讨论处理;(3)根据(2)问得出的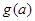 ,由
,由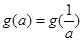 在对应区域上讨论解答即可.
在对应区域上讨论解答即可.
试题解析:(1)∵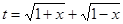 ,∴要使
,∴要使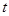 有意义,必须
有意义,必须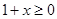 且
且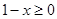 ,即
,即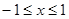 .
.
∵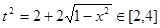 ,且
,且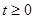 ①
①
∴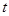 的取值范围是
的取值范围是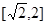 , 2分
, 2分
由①得: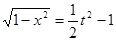 ,
,
∴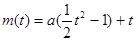
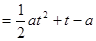 ,
,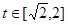 .
4分
.
4分
(2)由题意知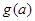 即为函数
即为函数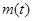
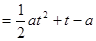 ,
,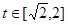 的最大值,
的最大值,
∵直线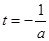 是抛物线
是抛物线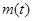
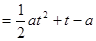 的对称轴,
5分
的对称轴,
5分
∴可分以下几种情况进行讨论:
①当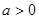 时,函数
时,函数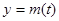 ,
,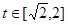 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由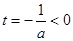 知
知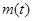 在
在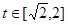 上单调递增,故
上单调递增,故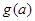
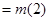
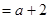 ;
;
②当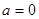 时,
时,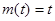 ,
,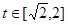 ,有
,有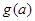 =2;
=2;
③当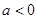 时,,函数
时,,函数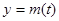 ,
,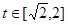 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若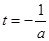
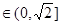 即
即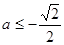 时,
时,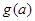
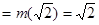 ,
,
若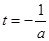
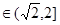 即
即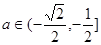 时,
时,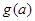
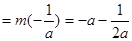 ,
,
若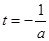
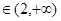 即
即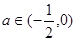 时,
时,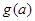
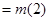
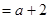 . 9分
. 9分
综上所述,有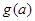 =
=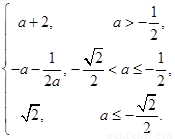 10分
10分
(3)当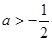 时,
时,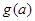
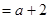
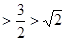 ;
;
当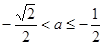 时,
时, ,
,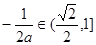 ,∴
,∴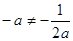 ,
,
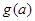
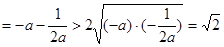 ,故当
,故当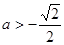 时,
时,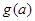
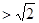 ;
;
当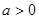 时,
时,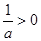 ,由
,由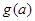
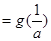 知:
知:
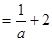 ,故
,故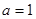 ;
;
当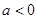 时,
时,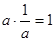 ,故
,故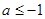 或
或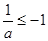 ,从而有
,从而有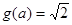 或
或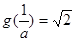 ,
,
要使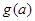
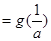 ,必须有
,必须有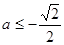 ,
, ,即
,即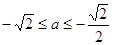 ,
,
此时,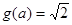
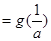 .
13分
.
13分
考点:1.分段函数;2.二次函数;3.函数最值.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
设a为实数,记函数![]() 的最大值为g(a).
的最大值为g(a).
(1)设t=![]() ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);
(2)求g(a);
(3)试求满足![]() 的所有实数a.
的所有实数a.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省嘉兴一中高一(上)期中数学试卷(解析版) 题型:解答题
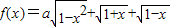 的最大值为g(a).
的最大值为g(a).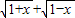 ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖南省长沙市周南中学高一(上)第一次月考数学试卷(解析版) 题型:解答题
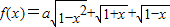 的最大值为g(a).
的最大值为g(a).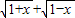 ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市江阴一中高一(上)第12周数学限时作业(解析版) 题型:解答题
 的最大值为g(a).
的最大值为g(a). ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com