练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】各国医疗科研机构都在研制某种病毒疫苗，现有G，E，F三个独立的医疗科研机构，它们在一定时期内能研制出疫苗的概率分别是.求：

    （1）他们都研制出疫苗的概率；

    （2）他们都失败的概率；

    （3）他们能够研制出疫苗的概率.

    【答案】（1）；（2）；（3）.

    【解析】

    （1）令事件分别表示G，E，F三个独立的医疗科研机构在一定时期内成功研制出该疫苗，这三个事件彼此独立，按照独立事件同时发生的概率求解；

    （2）都失败指同时发生，按照独立事件同时发生的概率求解；

    （3）与（2）是对立事件，根据对立事件概率公式求解.

    令事件分别表示G，E，F三个独立的医疗科研机构在一定时期内成功研制出该疫苗.

    依题意可知，事件相互独立，且.

    （1）他们都研制出疫苗，即事件同时发生，，即他们都研制出疫苗的概率为.

    （2）他们都失败，即事件同时发生，，即他们都失败的概率为.

    （3）“他们能够研制出疫苗”的对立事件为“他们都失败”，结合对立事件间的概率关系，可得所求事件的概率，即他们能研制出疫苗的概率为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知△ABC的三个内角A，B，C所对的边分别为a，b，c，向量=（sinA+sinC，sinB），=（c﹣b，c﹣a），且∥．

    （1）求角A的大小；

    （2）若a=3，b+c=5，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数函数与直线相切，设函数其中a、c∈R，e是自然对数的底数.

    （1）讨论h(x)的单调性；

    （2）h(x)在区间内有两个极值点.

    ①求a的取值范围；

    ②设函数h(x)的极大值和极小值的差为M，求实数M的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱柱的侧面是菱形，.

    （1） 求证：；

    （2）若，，，求的值，使得 二面角的余弦值的为 .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】全网传播的融合指数是衡量电视媒体在中国网民中影响力的综合指标，根据相关报道提供的全网传播2018年某全国性大型活动的“省级卫视新闻台”融合指数的数据，对名列前20名的“省级卫视新闻台”的融合指数进行分组统计，结果如表所示.

    组号

    分组

    频数

    1

    2

    2

    8

    3

    7

    4

    3

    现从融合指数在和内的“省级卫视新闻台”中随机抽取2家进行调研，求至少有1家的融合指数在内的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，菱形与正所在平面互相垂直，平面，，.

    （1）证明：平面；

    （2）若，求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l的参数方程为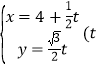为参数，以坐标原点为极点，x轴的正半轴为极轴建建立极坐标系，曲线C的极坐标方程为．

    求曲线C的直角坐标方程与直线l的极坐标方程；

    Ⅱ若直线与曲线C交于点不同于原点，与直线l交于点B，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.

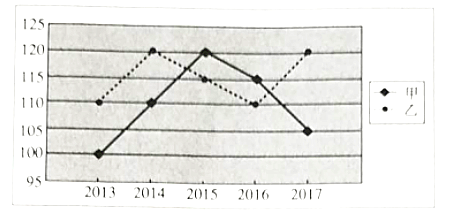
    （1）根据散点图，直接判断甲、乙这五年年度体检的血压值谁的波动更大，并求波动更大者的方差；

    （2）根据乙这五年年度体检血压值的数据，求年度体检血压值关于年份的线性回归方程，并据此估计乙在2018年年度体检的血压值.

    （附：，）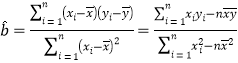

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有女子善织，日益功，疾，初日织五尺，今一月织七匹三丈（1匹=尺，一丈=尺），问日益几何？”其意思为：“有一女子擅长织布，每天比前一天更加用功，织布的速度也越来越快，从第二天起，每天比前一天多织相同量的布，第一天织尺，一月织了七匹三丈，问每天增加多少尺布？”若这一个月有天，记该女子一个月中的第天所织布的尺数为，则的值为（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案