为迎接夏季旅游旺季的到来,少林寺单独设置了一个专门安排游客住宿的客栈,寺庙的工作人员发现为游客准备的一些食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月人住的游客人数,发现每年各个月份来客栈人住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,人住客栈的游客人数基本相同;
②人住客栈的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份人住客栈的游客约为100人,随后逐月递增直到8月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问哪几个月份要准备400份以上的食物?
【答案】
分析:(1)根据①,可知函数的周期是12;根据②可知,f(2)最小,f(8)最大,且f(8)-f(2)=400;根据③可知,f(x)在[2,8]上单调递增,且f(2)=100,由此可得函数解析式;
(2)由条件知,200sin(
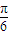
x
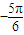
)+300≥400,结合x∈N
*,1≤x≤12,即可得到结论.
解答:解:(1)设该函数为f(x)=Asin(ωx+φ)+B(A>0,ω>0,0<|φ|<π)
根据①,可知函数的周期是12,∴
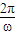
=12,∴ω=
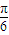
;
根据②可知,f(2)最小,f(8)最大,且f(8)-f(2)=400,故该函数的振幅为200;
根据③可知,f(x)在[2,8]上单调递增,且f(2)=100,∴f(8)=500
∴
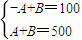
,∴
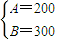
∵f(2)最小,f(8)最大,
∴sin(2×
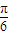
+φ)=-1,sin(8×
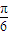
+φ)=1,
∵0<|φ|<π,
∴φ=
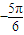
∴f(x)=200sin(
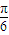
x
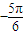
)+300;
(2)由条件知,200sin(
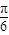
x
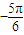
)+300≥400,化简可得sin(
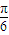
x
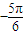
)
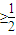
,
∴2kπ+
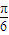
≤
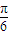
x
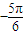
≤2kπ+
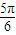
,k∈Z
∴12k+6≤x≤12k+10,k∈Z
∵x∈N
*,1≤x≤12
∴x=6,7,8,9,10
∴只有6,7,8,9,10五个月份要准备400份以上的食物.
点评:本题主要考查了在实际问题中建立三角函数模型的问题.解题的技巧是从问题中发现周期变化的规律,并将所发现的规律抽象为恰当的三角函数模型.

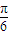 x
x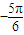 )+300≥400,结合x∈N*,1≤x≤12,即可得到结论.
)+300≥400,结合x∈N*,1≤x≤12,即可得到结论.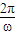 =12,∴ω=
=12,∴ω=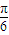 ;
;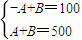 ,∴
,∴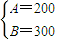
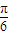 +φ)=-1,sin(8×
+φ)=-1,sin(8×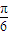 +φ)=1,
+φ)=1,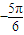
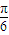 x
x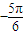 )+300;
)+300;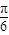 x
x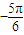 )+300≥400,化简可得sin(
)+300≥400,化简可得sin(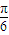 x
x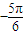 )
)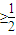 ,
,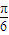 ≤
≤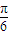 x
x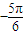 ≤2kπ+
≤2kπ+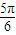 ,k∈Z
,k∈Z
