
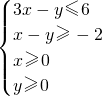 ,且目标函数z=ax+by(a>0,b>0)的最大值为12,则
,且目标函数z=ax+by(a>0,b>0)的最大值为12,则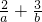 的最小值为________.
的最小值为________. 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:高中数学 来源: 题型:
| f(x1)-f(x2) |
| x1-x2 |
| y |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2008-2009学年重庆一中高三(上)10月月考数学试卷(理科)(解析版) 题型:填空题
 ,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时, 的取值范围为 .
的取值范围为 .查看答案和解析>>
科目:高中数学 来源:2012年山东省实验中学高考数学三模试卷(文科)(解析版) 题型:填空题
 ,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时, 的取值范围为 .
的取值范围为 .查看答案和解析>>
科目:高中数学 来源:2013年山东省淄博市高考数学模拟试卷3(理科)(解析版) 题型:填空题
 ,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时, 的取值范围为 .
的取值范围为 .查看答案和解析>>
科目:高中数学 来源:2012年山东省实验中学高考数学三模试卷(理科)(解析版) 题型:解答题
 ,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时, 的取值范围为 .
的取值范围为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com