Question

已知数列｛a_n｝的前n项和S_n=2a_n+1，求证：｛a_n｝是等比数列，并求出其通项公式.

Answer 1

思路解析：要想证数列是等比数列，只需看a_n+1与a_n之比是否为同一常

数.由题设条件还要利用a_n+1=S_n+1-S_n，求得a_n+1.

证明：∵S_n=2a_n+1，

∴S_n+1=2a_n+1+1.

则a_n+1=S_n+1-S_n=（2a_n+1+1）-（2a_n+1）=2a_n+1-2a_n，

可得a_n+1=2a_n.                                                                 ①

又∵S₁=a₁=2a₁+1，

∴a₁=-1≠0.

并且由①式可知a_n≠0.

因此，由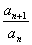=2，可知｛a_n｝是等比数列，a₁=-1，q=2.

∴a_n=a₁q^n-1=-2^n-1.

深化升华

判断或证明一个数列是等比数列的常用方法是根据等比数列的概念，证明对任意自然数n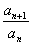，都等于同一个常数.