
分析 (1)根据直线方程为y=mx+(3-4m),得m(x-4)+3-y=0,x-4=0且3-y=0,即可证明直线必过定点;
(2)要使面积最小则定点一定在圆上,此时易求出圆的方程;
(3)根据圆与x轴相交,求出AB两点坐标,根据P在圆内以及由$\overrightarrow{PO}$2=|$\overrightarrow{PA}$|•|$\overrightarrow{PB}$|,分别求出一个关系式,两个关系式联立即可求出y02的取值范围,最终判断出$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围.
解答 (1)证明:∵直线方程为y=mx+(3-4m),
∴m(x-4)+3-y=0,
∴x-4=0且3-y=0,
∴得l过定点T(4,3)
(2)解:由题意,要使圆O的面积最小,定点T(4,3)在圆上
∴圆O的方程为:x2+y2=25
(3)解:∵圆O与x轴相交于A、B两点,
故A(-5,0)B(5,0)
设P(x0,y0)为圆内任意一点
故:x02+y02<25 ①
$\overrightarrow{PA}$=(-5-x0,-y0),$\overrightarrow{PB}$=(5-x0,y0),
由$\overrightarrow{PO}$2=|$\overrightarrow{PA}$|•|$\overrightarrow{PB}$|,∴x02+y02=$\sqrt{({x}_{0}+5)^{2}+{{y}_{0}}^{2}}$•$\sqrt{({x}_{0}-5)^{2}+{{y}_{0}}^{2}}$
整理得:x02-y02=$\frac{25}{2}$ ②
由①②得:0≤y02≤$\frac{25}{4}$
$\overrightarrow{PA}$•$\overrightarrow{PB}$=(x02-25)+y02=2y02-$\frac{25}{2}$
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$∈[-$\frac{25}{2}$,0).
点评 本题考查向量的取值范围问题,涉及到直线与圆的位置关系,以及等比数列问题.通过圆内任意点坐标满足的两个关系最终确定向量的取值范围,属于难题.


科目:高中数学 来源: 题型:解答题
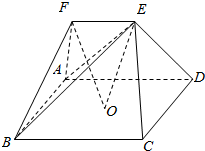 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF是等边三角形,棱EF∥BC,且EF=$\frac{1}{2}$BC.
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF是等边三角形,棱EF∥BC,且EF=$\frac{1}{2}$BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-9,9] | B. | [-12,12] | C. | [-15,15] | D. | [-18,18] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com