
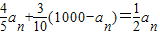 +300.所以an+1-600=
+300.所以an+1-600=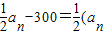 -600),由此能求出当a1=a时的通项an.
-600),由此能求出当a1=a时的通项an.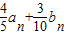 (3分)
(3分)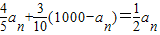 +300(5分)
+300(5分) -600)
-600) 的等比数列(9分)
的等比数列(9分) )n-1(11分)
)n-1(11分) )n-1.(12分)
)n-1.(12分)

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)学校餐厅每天供应1000名学生用餐,每星期一有A、B两样特色菜可供选择(每个学生都将从二者中选一),调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A![]() 、B
、B![]() 分别表示在第n个星期一选A、B菜的人数。(1)试以A
分别表示在第n个星期一选A、B菜的人数。(1)试以A![]() 表示A
表示A![]() ;(2)若A
;(2)若A![]() =200,求{A
=200,求{A![]() }的通项公式;(3)问第n个星期一时,选A与选B的人数相等?
}的通项公式;(3)问第n个星期一时,选A与选B的人数相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com