Question

一块正方形薄铁皮的边长为4，以它的一个顶点为圆心，剪下一个最大的扇形，用这块扇形围成一个圆锥，则这个圆锥的容积等于     ．

Answer 1

【答案】分析：说明扇形何时最大，就是周长的圆弧，求出圆锥的底面半径和高，即可求出圆锥的体积．
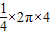
解答：解：所画扇形是以R=4为半径的圆的周长的圆弧，所以=2π．∵2π又为圆锥的底面圆的周长∴圆锥底面半径r=1∵圆锥的高h²=R²-r²，解得h=
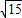
∴圆锥的容积v=πr²h=．
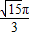
故答案为：
点评：本题是基础题，考查圆锥的侧面展开图，扇形的弧长问题，特征的体积的求法，考查空间想象能力，计算能力，常考题型．