
已知正四棱锥P-ABCD中,底面是边长为2 的正方形,高为![]() .M为线段PC的中点.
.M为线段PC的中点.
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.
 |
本题主要考查空间点、线、面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力。满分14分。
(Ⅰ)证明:在四棱锥P-ABCD中,连结AC交BD于点O,连结OM,PO.由条件可得PO=![]() ,AC=2
,AC=2![]() ,PA=PC=2,CO=AO=
,PA=PC=2,CO=AO=![]() .
.
 |
因为在△PAC中,M为PC的中点,O为AC的中点,
所以OM为△PAC的中位线,得OM∥AP,
又因为AP![]() 平面MDB,OM
平面MDB,OM![]() 平面MDB,
平面MDB,
所以PA∥平面MDB. …………6分
(Ⅱ) 解:设NC∩MO=E,由题意得BP=BC=2,且∠CPN=90°.
因为M为PC的中点,所以PC⊥BM,
同理PC⊥DM,故PC⊥平面BMD.
所以直线CN在平面BMD内的射影为直线OM,∠MEC为直线CN与平面BMD所成的角,
又因为OM∥PA,所以∠PNC=∠MEC.
在Rt△CPN中,CP=2,NP=1,所以tan∠PNC=![]() ,
,
故直线 CN与平面BMD所成角的正切值为2. …………14分


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
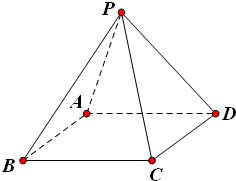 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
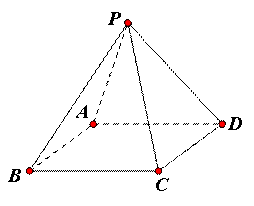 (1)用h表示底面边长,并求正四棱锥体积V的最大值;
(1)用h表示底面边长,并求正四棱锥体积V的最大值;
(2)当![]() 取最大值时,求异面直线AB和PD所成角的大小.
取最大值时,求异面直线AB和PD所成角的大小.
(结果用反三角函数值表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com