Question

设f(x)是定义在R上的偶函数，对x∈R，都有f(x+4)=f(x)，且当x∈[－2,0]时，f(x)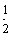＝()^x－1，若在区间(－2，6]内关于x的方程f(x)－log_a(x＋2)＝0(a＞1)恰有3个不同的实数根，则a的取值范围是

A．(1,2)             B．(2，＋∞)         C．(1,)          D．(,2)

 

Answer 1

【答案】

D

【解析】

试题分析：由已知中可以得到函数f（x）是一个周期函数，且周期为4，将方程f（x）-log_a^x+2=0恰有3个不同的实数解，转化为函数f（x）的与函数y=-log_a^x+2的图象恰有3个不同的交点，数形结合即可得到实数a的取值范围．解：∵对于任意的x∈R，都有f（x-2）=f（2+x），∴函数f（x）是一个周期函数，且T=4．又∵当x∈[-2，0]时，f（x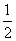）=（ ）^x-1，且函数f（x）是定义在R上的偶函数，若在区间（-2，6]内关于x的方程f（x）-log_a（x+2）=0恰有3个不同的实数解，则函数y=f（x）与y=log_a（x+2）在区间（-2，6]上有三个不同的交点，如下图所示：

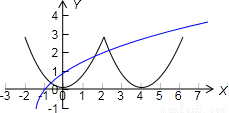
又f（-2）=f（2）=3，则有 log_a4＜3，且log_a8＞3，解得：

＜a＜2，故答案为 D

考点：函数的零点

点评：本题考查的知识点是根的存在性及根的个数判断，指数函数与对数函数的图象与性质，其中根据方程的解与函数的零点之间的关系，将方程根的问题转化为函数零点问题，是解答本题的关键，体现了转化和数形结合的数学思想，属于中档题．