
设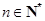 且
且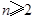 ,证明:
,证明:


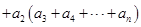

 .
.
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:
(本小题满分14分)已知递增数列![]() 满足:
满足:![]() ,
,![]()
![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列。(I)求数列
成等比数列。(I)求数列![]() 的通项公式
的通项公式![]() ;(II)若数列
;(II)若数列![]() 满足:
满足:![]()
![]() ,且
,且![]() 。①证明数列
。①证明数列![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式
的通项公式![]() ;②设
;②设![]() ,数列
,数列![]() 前
前![]() 项和为
项和为![]() ,
,
![]() ,
,![]() 。当
。当![]() 时,试比较A与B的大小。
时,试比较A与B的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分16分)已知二次函数g(x)对任意实数x都满足![]() ,且
,且![]() .令
.令![]() .
.
(1)求 g(x)的表达式;
(2)若![]() 使
使![]() 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)设![]() ,
,![]() ,证明:对
,证明:对![]() ,恒有
,恒有![]()
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建师大附中高二第二学期模块考试理科数学 题型:解答题
(本小题15分)
设数列{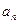 }的前n项和为
}的前n项和为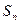 ,并且满足
,并且满足 ,
,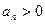 (n∈N*).
(n∈N*).
(Ⅰ)求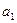 ,
,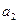 ,
,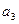 ;
;
(Ⅱ)猜想{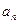 }的通项公式,并用数学归纳法加以证明;
}的通项公式,并用数学归纳法加以证明;
(Ⅲ)设 ,
,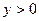 ,且
,且 ,证明:
,证明: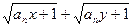 ≤
≤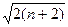 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市东城区高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题共13分)已知椭圆 的右焦点为
的右焦点为 ,
,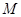 为椭圆的上顶点,
为椭圆的上顶点, 为坐标原点,且△
为坐标原点,且△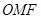 是等腰直角三角形.
是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点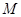 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于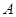 ,
,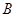 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为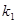 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点(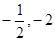 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com