Question

【题目】已知f（x）=|x﹣a|，a∈R．
（1）当a=1时，求不等式f（x）+|2x﹣5|≥6的解集；
（2）若函数g（x）=f（x）﹣|x﹣3|的值域为A，且[﹣1，2]A，求a的取值范围．

Answer 1

【答案】
（1）解：a=1时，|x﹣1|+|2x﹣5|≥6，

x≤1时：1﹣x﹣2x+5≥6，解得：x≤0，∴x≤0，

1＜x＜2.5时：x﹣1﹣2x+5≥6，解得：x≤﹣1，不成立；

x≥2.5时：x﹣1+2x﹣5≥6，解得：x≥4，∴x≥4，

故不等式的解集是{x|x≥4或x≤0}

（2）解：g（x）=|x﹣a|﹣|x﹣3|，

a≥3时：g（x）= ，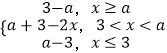

∴3﹣a≤g（x）≤a﹣3，

∵[﹣1，2]A，∴ ，解得a≥5；

a＜3时，a﹣3≤g（x）≤3﹣a，

∴ ，解得：a≤1；

综上：a≤1或a≥5

【解析】（1）将a=1代入f（x），通过讨论x的范围求出各个区间上的x的范围，取并集即可；（2）通过讨论a的范围，得到关于a的不等式组，解出即可．