
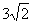 ;
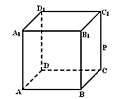
;| 解:(1)连AC,设AC与BD相交于点O,AP与平面BDD1B1相交于点G, 连结OG,因为 PC∥平面 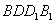 ,平面BDD1B1∩平面APC=OG, ,平面BDD1B1∩平面APC=OG,故OG∥PC,所以,OG= 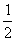 PC= PC=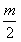 , ,又AO⊥BD,AO⊥BB1, 所以AO⊥平面 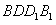 , ,故∠AGO是AP与平面 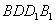 所成的角。 所成的角。 在Rt△AOG中,tan∠AGO= 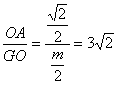 , ,即m= 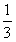 , ,所以当m= 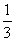 时,直线AP与平面 时,直线AP与平面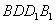 所成的角的正切值为 所成的角的正切值为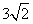 。 。 |
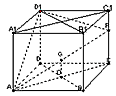 |
| (2)可以推测,点Q应当是A1C1的中点O1, 因为 D1O1⊥A1C1,且 D1O1⊥A1A , 所以 D1O1⊥平面ACC1A1, 又AP 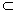 平面ACC1A1, 平面ACC1A1,故 D1O1⊥AP, 那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直。 |


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:高中数学 来源: 题型:
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.查看答案和解析>>
科目:高中数学 来源:2009-2010学年江苏省南京市金陵中学高三(上)8月月考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2012年安徽省合肥八中高考数学一模试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com