设函数f(x)=kx2-kx-6+k.
(1)若对于k∈[-2,2],f(x)<0恒成立,求实数x的取值范围.
(2)若对于x∈[1,2],f(x)<0恒成立,求实数k的取值范围.
分析:(1)根据对于k∈[-2,2],f(x)<0恒成立,变更主元k(x
2-x+1)-6=g(k),可得
| | g(2)=2x2-2x-4<0 | | g(-2)=-2x2+2x-8<0 |
| |
,解此不等式组即可求得结果;
(2)法1:要使f(x)=k(x
2-x+1)-6<0在x∈[1,2]上恒成立,则只须
k<在x∈[1,2]上恒成立;求得
的最小值即可;
法2:配方,分类讨论∴
或
或
,即可求得结果.
解答:解:(1)设f(x)=k(x
2-x+1)-6=g(k),
则g(k)是关于k的一次函数,且一次项系数为x
2-x+1…(2分)
法1、∵
x2-x+1=(x-)2+>0∴g(k)在[-2,2]上递增.…(4分)
∴g(k)<0?g(2)=2(x
2-x+1)-6<0∴解得x的取值范围为:-1<x<2…(6分)
法2、依题只须
| | g(2)=2x2-2x-4<0 | | g(-2)=-2x2+2x-8<0 |
| |
?∴-1<x<2
(2)法1、要使f(x)=k(x
2-x+1)-6<0在x∈[1,2]上恒成立
则只须
k<在x∈[1,2]上恒成立;…(8分)
而当x∈[1,2]时:
=≥=2…(10分)
∴k<2…(12分)
法2、∵
f(x)=k(x-)2+k-6<0在x∈[1,2]上恒成立
∴
或
或
综上解得:k<2
点评:本题考查二次函数的图象和性质,解题时要抓住二次函数与x轴无交点的特点进行求解.主要考查了二次函数的恒成立问题.二次函数的恒成立问题分两类,一是大于0恒成立须满足开口向上,且判别式小于0,二是小于0恒成立须满足开口向下,且判别式小于0.属中档题.



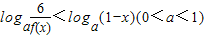 的解集.
的解集.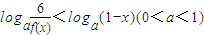 的解集.
的解集.