
【题目】在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,则三棱锥
,则三棱锥![]() 外接球的体积的最小值为( )
外接球的体积的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】里氏震级M的计算公式为:M=lgA﹣lgA0,其中A是测震仪记录的地震曲线的最大振幅,是相应的标准地震的振幅,假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅A0为0.001,则此次地震的震级为 级;9级地震的最大的振幅是5级地震最大振幅的 倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本![]() (元)与生产该产品的数量
(元)与生产该产品的数量![]() (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根据以上数据,绘制了散点图.
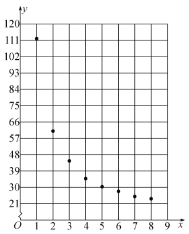
观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型![]() 和指数函数模型
和指数函数模型![]() 分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为
分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为![]() ,
,![]() 与
与![]() 的相关系数
的相关系数![]() .
.
参考数据(其中![]() ):
):
|
|
|
|
|
|
|
|
183.4 | 0.34 | 0.115 | 1.53 | 360 | 22385.5 | 61.4 | 0.135 |
(1)用反比例函数模型求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本;
(3)该企业采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为100元,则签订9千件订单的概率为0.8,签订10千件订单的概率为0.2;若单价定为90元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为10元,根据(2)的结果,企业要想获得更高利润,产品单价应选择100元还是90元,请说明理由.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: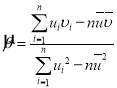 ,
,![]() ,相关系数
,相关系数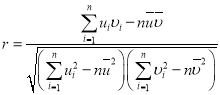 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为![]() ,半径为
,半径为![]() ,该纸片上的正方形
,该纸片上的正方形![]() 的中心为
的中心为![]() 为圆
为圆![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() ,
,![]() 分别是以
分别是以![]() 为底边的等腰三角形.沿虚线剪开后,分别以
为底边的等腰三角形.沿虚线剪开后,分别以![]() 为折痕折起
为折痕折起![]() ,
,![]() ,
,![]() ,
,![]() 使得
使得![]() 重合,得到一个四棱锥.当该四棱锥的侧面积是底面积的2倍时,该四棱锥的外接球的表面积为__________.
重合,得到一个四棱锥.当该四棱锥的侧面积是底面积的2倍时,该四棱锥的外接球的表面积为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=2,AD=1.将矩形沿对角线BD折起,使A移到点P,P在平面BCD上的投影O恰好落在CD边上.
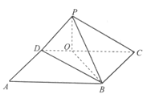
(1)证明:DP⊥平面BCP;
(2)求点O到平面PBD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣x﹣alnx.
(1)当a=3时,求f(x)在[1,2]上的最大值与最小值;
(2)若f(x)在(0,+∞)上单调递增,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com